题目内容
15.点P( 1,4,-3)与点Q(3,-2,5)的中点坐标是( )| A. | ( 4,2,2) | B. | (2,-1,2) | C. | (2,1,1) | D. | ( 4,-1,2) |
分析 直接利用空间中点坐标公式求解即可.
解答 解:点P( 1,4,-3)与点Q(3,-2,5)的中点坐标是:(2,1,1).
故选:C.
点评 本题考查空间中点坐标公式的应用,是基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
5.组合数$C_n^m+2C_n^{m-1}+C_n^{m-2}$(n≥m≥2,m,n∈N*)恒等于( )
| A. | $C_{n+2}^m$ | B. | $C_{n+2}^{m+1}$ | C. | $C_{n+1}^m$ | D. | $C_{n+1}^{m+1}$ |
3.“直线l1、l2互相垂直”是“直线l1、l2的斜率之积等于-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
20.点P( 1,4,-3)与点Q(3,-2,5)的中点坐标是( )
| A. | ( 4,2,2) | B. | (2,-1,2) | C. | (2,1,1) | D. | 4,-1,2) |
7.下列条件能唯一确定一个平面的是( )
| A. | 空间任意三点 | B. | 不共线三点 | C. | 共线三点 | D. | 两条异面直线 |
4.已知A(1,0)、B(2,-1),若点P(x,y)满足x+y+1=0,则|PA|+|PB|的最小值为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
5.对于两个平面α,β和两条直线m,n,下列命题中真命题是( )
| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,α⊥β,则m⊥β | ||
| C. | 若m∥α,n∥β,α⊥β,则m⊥n | D. | 若m⊥α,n⊥β,α⊥β,则m⊥n |
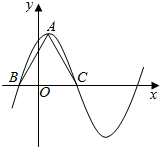 函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象
函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象