��Ŀ����
12����֪����$\overrightarrow m=��\sqrt{2}cos\frac{x}{4}��2cos\frac{x}{4}��$��$\overrightarrow n=��\sqrt{2}cos\frac{x}{4}��\sqrt{3}sin\frac{x}{4}��$����$f��x��=\overrightarrow m•\overrightarrow n$��������f������=2����$cos����+\frac{��}{3}��$��ֵ��
�����ڡ�ABC�У���A��B��C�ĶԱ߷ֱ���a��b��c�������㣨2a-b��cosC=ccosB����f��A����ȡֵ��Χ��
���� ������$f��x��=\overrightarrow m•\overrightarrow n$���������������������������f��x���Ľ���ʽ��f������=2���ҳ���$cos����+\frac{��}{3}��$�Ĺ�ϵ���ɵý⣮
�����������Ҷ����������C�ǵĴ�С��������Ǻ�����������⼴�ɣ�
��� �⣺��������$\overrightarrow m=��\sqrt{2}cos\frac{x}{4}��2cos\frac{x}{4}��$��$\overrightarrow n=��\sqrt{2}cos\frac{x}{4}��\sqrt{3}sin\frac{x}{4}��$��
��$f��x��=\overrightarrow m•\overrightarrow n$
��ô��$f��x��=2{cos^2}\frac{x}{4}+2\sqrt{3}sin\frac{x}{4}cos\frac{x}{4}$=$\sqrt{3}sin\frac{x}{2}+cos\frac{x}{2}+1$=$2sin��\frac{x}{2}+\frac{��}{6}��+1$��
��f������=2����$sin��\frac{��}{2}+\frac{��}{6}��$=$\frac{1}{2}$��
��$cos����+\frac{��}{3}��=1-2{sin^2}��\frac{��}{2}+\frac{��}{6}��=\frac{1}{2}$��
���ߣ�2a-b��cosC=ccosB��
�ࣨ2sinA-sinB��cosC=sinCcosB��
⇒2sinAcosC=sinBcosC+cosBsinC=sin��B+C����
��2sinAcosC=sinA��
��sinA��0��
��$cosC=\frac{1}{2}$����$C=\frac{��}{3}$��
��$0��A��\frac{2��}{3}$��
$\frac{��}{6}��\frac{A}{2}+\frac{��}{6}��\frac{��}{2}$��
��$\frac{1}{2}��sin��\frac{A}{2}+\frac{��}{6}����1$��
��$f��A��=2sin��\frac{A}{2}+\frac{��}{6}��+1$��
��f��A����ȡֵ��ΧΪ��2��3����
���� ������Ҫ��������Ǻ����Ļ������������Ǻ�����ͼ������ʵ����ã��������Ǻ�����ʽ���������л����ǽ������Ĺؼ��������е��⣮

 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�| ��λְ���ijɼ����֣� | 87 | 88 | 91 | 91 | 93 |
| �ҵ�λְ���ijɼ����֣� | 85 | 89 | 91 | 92 | 93 |
��2���ü���������ķ������ҵ�λ��5��ְ���г�ȡ2�������ǵijɼ����һ�����������ȡ��2��ְ���ijɼ�֮��ľ���ֵ������4�ֵĸ��ʣ�
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{5}$ |
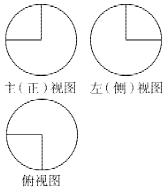 ��ͼ��ij�����������ͼ�������뾶��ȵ�Բ��ÿ��Բ���������ֱ�İ뾶�����ü�����ı������17�У�����������ǣ�������
��ͼ��ij�����������ͼ�������뾶��ȵ�Բ��ÿ��Բ���������ֱ�İ뾶�����ü�����ı������17�У�����������ǣ�������| A�� | 8�� | B�� | $\frac{56��}{3}$ | C�� | $\frac{14��}{3}$ | D�� | $\frac{28��}{3}$ |
| A�� | 4 | B�� | 6 | C�� | 12 | D�� | 16 |
| A�� | 3 | B�� | 4 | C�� | 7 | D�� | 8 |
| A�� | -1 | B�� | -2 | C�� | 1 | D�� | 2 |
| A�� | ? | B�� | 0 | C�� | {0} | D�� | {-1��1} |