题目内容
如图, 四棱柱ABCD－A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,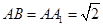 
.
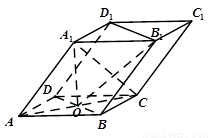
(Ⅰ) 证明: A1C⊥平面BB1D1D;
(Ⅱ) 求平面OCB1与平面BB1D1D的夹角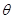
的大小.
【答案】
(Ⅰ) 见解析(Ⅱ) 所求夹角的大小为
【解析】如图建立空间直角坐标系，
由
可知
(Ⅰ)
, 
,
,即
，且
所以
（Ⅱ）容易求得平面
的一个法向量为
，平面
的一个法向量为
，所求夹角余弦值为
.所求夹角的大小为.
本题考查空间直线与平面的位置关系和二面角问题，考查空间想象能力和推理论证能力、对公式的熟练准确运用.此类问题的易错点是未能合理的建立空间直角坐标系，找好线面的垂直关系.空间向量的解决对法向量求解不准确，二面角的锐角和钝角判断不准会导致结果错误.
【考点定位】本题考查空间直线现平面的位置关系和二面角问题，考查空间想象能力和推理论证能力.
练习册系列答案
文敬图书课时先锋系列答案
相关题目
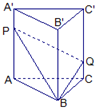如图直三棱柱ABC-A1B1C1的体积为V，点P、Q分别在侧棱AA1和CC1上，AP=C1Q，则四棱锥B-APQC的体积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
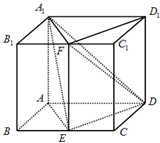如图，四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形，且AA1⊥底面ABCD，AB=2，AA1=BC=4，∠ABC=60°，点E为BC中点，点F为B1C1中点．
如图：三棱柱ABC-A1B1C1中，AB=AC=BC=2，AA1=3，侧棱AA1⊥底面ABC，D为C1B的中点，P为AB边上的动点．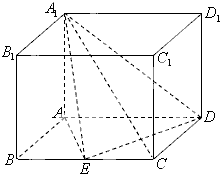
如图，四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形，且AB=1，BC=2，∠ABC=60°，E为BC的中点，AA1⊥平面ABCD．
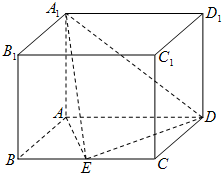（2012•江门一模）如图，四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形，且AB=1，BC=2，∠ABC=60°，E为BC的中点，AA1⊥平面ABCD．