题目内容
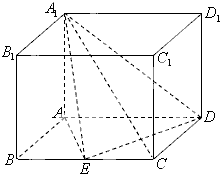 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD.(Ⅰ)证明:平面A1AE⊥平面A1DE;
(Ⅱ)若DE=A1E,试求异面直线AE与A1D所成角的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试求二面角C-A1D-E的余弦值.
分析:(1)根据题意,得△ABE是正三角形,∠AEB=60°,等腰△CDE中∠CED=
(180°-∠ECD)=30°,所以∠AED=90°,得到DE⊥AE,结合DE⊥AA1,得DE⊥平面A1AE,从而得到平面A1AE⊥平面平面A1DE.
(2)取BB1的中点F,连接EF、AF,连接B1C.证出EF∥A1D,可得∠AEF(或其补角)是异面直线AE与A1D所成的角.利用勾股定理和三角形中位线定理,算出△AEF各边的长,再用余弦定理可算出异面直线AE与A1D所成角的余弦值.
(3)建立的空间直角坐标系中,求得平面A1DE的一个法向量,平面CA1D的法向量,利用向量数量积求解夹角余弦值,则易得二面角C-A1D-E的余弦值.
| 1 |
| 2 |
(2)取BB1的中点F,连接EF、AF,连接B1C.证出EF∥A1D,可得∠AEF(或其补角)是异面直线AE与A1D所成的角.利用勾股定理和三角形中位线定理,算出△AEF各边的长,再用余弦定理可算出异面直线AE与A1D所成角的余弦值.
(3)建立的空间直角坐标系中,求得平面A1DE的一个法向量,平面CA1D的法向量,利用向量数量积求解夹角余弦值,则易得二面角C-A1D-E的余弦值.
解答:解:(1)依题意,BE=EC=
BC=AB=CD,
∴△ABE是正三角形,∠AEB=60°,
又∵△CDE中,∠CED=∠CDE=
(180°-∠ECD)=30°
∴∠AED=180°-∠CED-∠AEB=90°,即DE⊥AE,
∵AA1⊥平面ABCD,DE⊆平面ABCD,∴DE⊥AA1,
∵AA1∩AE=A,∴DE⊥平面A1AE,
∵DE⊆平面A1DE,∴平面A1AE⊥平面A1DE.
(2)取BB1的中点F,连接EF、AF,连接B1C,
∵△BB1C中,EF是中位线,∴EF∥B1C
∵A1B1∥AB∥CD,A1B1=AB=CD,
∴四边形ABCD是平行四边形,可得B1C∥A1D
∴EF∥A1D,
可得∠AEF(或其补角)是异面直线AE与A1D所成的角.
∵△CDE中,DE=
CD=
=A1E=
,AE=AB=1
∴A1A=
,由此可得BF=
,AF=EF=
=
,
∴cos∠AEF=
=
,即异面直线AE与A1D所成角的余弦值为
(Ⅲ)取BE的中点F,以A为原点,AF所在直线为x轴,AD所在直线为y轴,AA1所在直线为z轴建立空间直角坐标系,AA1=
则A(0,0,0),D(0,2,0),C(
,
,0),
A1(0,0,
),
又
=(-
,
,0),
=(0,2,-
)
设平面CA1D的法向量
=(x,y,z)
则
得
=(1,
,
),
同理可得平面A1DE的一个法向量为
=(
,1,
)
设二面角C-A1D-E的平面角为θ,且θ为锐角
则cosθ=|cos<
,
>|=
=
=
所以二面角C-A1D-E的余弦值为
.
| 1 |
| 2 |
∴△ABE是正三角形,∠AEB=60°,
又∵△CDE中,∠CED=∠CDE=
| 1 |
| 2 |

∴∠AED=180°-∠CED-∠AEB=90°,即DE⊥AE,
∵AA1⊥平面ABCD,DE⊆平面ABCD,∴DE⊥AA1,
∵AA1∩AE=A,∴DE⊥平面A1AE,
∵DE⊆平面A1DE,∴平面A1AE⊥平面A1DE.
(2)取BB1的中点F,连接EF、AF,连接B1C,
∵△BB1C中,EF是中位线,∴EF∥B1C
∵A1B1∥AB∥CD,A1B1=AB=CD,
∴四边形ABCD是平行四边形,可得B1C∥A1D
∴EF∥A1D,
可得∠AEF(或其补角)是异面直线AE与A1D所成的角.
∵△CDE中,DE=
| 3 |
| 3 |
| A1A2+AE2 |
∴A1A=
| 2 |
| ||
| 2 |
|
| ||
| 2 |
∴cos∠AEF=
| AE2+EF2-AF2 |
| 2×AE×EF |
| ||
| 6 |
| ||
| 6 |
(Ⅲ)取BE的中点F,以A为原点,AF所在直线为x轴,AD所在直线为y轴,AA1所在直线为z轴建立空间直角坐标系,AA1=
| 2 |
则A(0,0,0),D(0,2,0),C(
| ||
| 2 |
| 3 |
| 2 |
A1(0,0,
| 2 |
又
| CD |
| ||
| 2 |
| 1 |
| 2 |
| A1D |
| 2 |

设平面CA1D的法向量
| n3 |
则
|
| n3 |
| 3 |
| 6 |
同理可得平面A1DE的一个法向量为
| n2 |
| 3 |
| 2 |
设二面角C-A1D-E的平面角为θ,且θ为锐角
则cosθ=|cos<
| n2 |
| n3 |
| ||||
|
|
4
| ||||
|
2
| ||
| 5 |
所以二面角C-A1D-E的余弦值为
2
| ||
| 5 |
点评:本题在直平行六面体中,求证面面垂直并求异面直线所成角余弦,着重考查了线面垂直、面面垂直的判定与性质和异面直线所成角的求法等知识,属于中档题.

练习册系列答案
相关题目
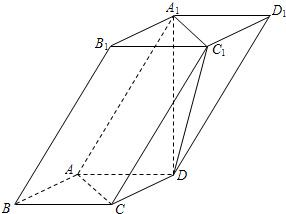 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.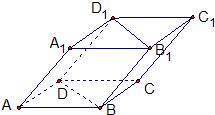 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是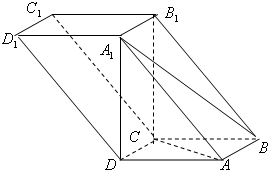 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,