题目内容
 如图:三棱柱ABC-A1B1C1中,AB=AC=BC=2,AA1=3,侧棱AA1⊥底面ABC,D为C1B的中点,P为AB边上的动点.
如图:三棱柱ABC-A1B1C1中,AB=AC=BC=2,AA1=3,侧棱AA1⊥底面ABC,D为C1B的中点,P为AB边上的动点.(1)若P为AB中点,求证:PD∥平面ACC1A1
(2)若DP⊥AB,求四棱锥P-ACC1A1的体积.
分析:(1)P为AB中点,连结AC1,证明PD∥AC1,利用直线与平面平行的判定定理证明PD∥平面ACC1A1
(2)若DP⊥AB,求四棱锥P-ACC1A1的体积.
(2)若DP⊥AB,求四棱锥P-ACC1A1的体积.
解答: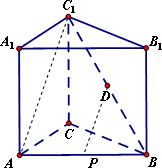 解:(1)证明:P为AB中点,连结AC1,因为D为C1B的中点,所以PD是三角形ABC1的中位线,所以PD∥AC1,AC1?平面ACC1A1,由直线与平面平行的判定定理,可知PD∥平面ACC1A1
解:(1)证明:P为AB中点,连结AC1,因为D为C1B的中点,所以PD是三角形ABC1的中位线,所以PD∥AC1,AC1?平面ACC1A1,由直线与平面平行的判定定理,可知PD∥平面ACC1A1
(2)三棱柱ABC-A1B1C1中,AB=AC=BC=2,DP⊥AB,
∴AP=3PB,解得BP=
,
又AA1=3,侧棱AA1⊥底面ABC,AC1=
,
所以四棱锥P-ACC1A1的体积,VP-ACC1A1=
VB-ACC1A1=
×
×2×3×
=
.
 解:(1)证明:P为AB中点,连结AC1,因为D为C1B的中点,所以PD是三角形ABC1的中位线,所以PD∥AC1,AC1?平面ACC1A1,由直线与平面平行的判定定理,可知PD∥平面ACC1A1
解:(1)证明:P为AB中点,连结AC1,因为D为C1B的中点,所以PD是三角形ABC1的中位线,所以PD∥AC1,AC1?平面ACC1A1,由直线与平面平行的判定定理,可知PD∥平面ACC1A1(2)三棱柱ABC-A1B1C1中,AB=AC=BC=2,DP⊥AB,
∴AP=3PB,解得BP=
| 1 |
| 2 |
又AA1=3,侧棱AA1⊥底面ABC,AC1=
| 13 |
所以四棱锥P-ACC1A1的体积,VP-ACC1A1=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
3
| ||
| 2 |
点评:本题考查直线与平面平行的判定定理,几何体的体积的求法,考查计算能力、空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=