题目内容
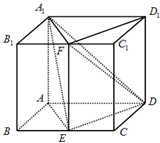 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.(Ⅰ)求证:平面A1ED⊥平面A1AEF;
(Ⅱ)求三棱锥E-A1FD的体积.
分析:(Ⅰ)由已知中AB=2,BC=4,∠ABC=60°,点E为BC中点,我们易得到∠AEB=60°,∠CED=30°,进而得到AE⊥ED,又由AA1⊥底面ABCD,得AA1⊥ED,结合线面垂直的判定定理得到ED⊥平面AA1EF,再由面面垂直的判定定理,即可得到平面A1ED⊥平面A1AEF;
(Ⅱ)将三棱锥E-A1FD的体积转化为三棱锥D-A1FE的体积,求出棱锥的高及底面面积,代入棱锥体积公式,即可得到答案.
(Ⅱ)将三棱锥E-A1FD的体积转化为三棱锥D-A1FE的体积,求出棱锥的高及底面面积,代入棱锥体积公式,即可得到答案.
解答:解:(Ⅰ)证明:∵AB=2,BC=4,∠ABC=60°,点E为BC中点,
∴△ABC为等边三角形,∠AEB=60°
△CDE中,∠CED=30°
∴AE⊥ED
∵AA1⊥底面ABCD,
∴AA1⊥ED,
又由AE∩AA1=A
∴ED⊥平面AA1EF
又∵ED?平面A1ED
∴平面A1ED⊥平面A1AEF;
(Ⅱ)三棱锥E-A1FD的体积与三棱锥D-A1FE的体积相等
其中DE为棱锥的高,
又∵DE=AD•sin30°=2
∴V=
•(
×2×4)•2
=
∴△ABC为等边三角形,∠AEB=60°
△CDE中,∠CED=30°
∴AE⊥ED
∵AA1⊥底面ABCD,
∴AA1⊥ED,
又由AE∩AA1=A
∴ED⊥平面AA1EF
又∵ED?平面A1ED
∴平面A1ED⊥平面A1AEF;
(Ⅱ)三棱锥E-A1FD的体积与三棱锥D-A1FE的体积相等
其中DE为棱锥的高,
又∵DE=AD•sin30°=2
| 3 |
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
8
| ||
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,其中根据AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,结合等腰三角形性质,得到AE⊥ED,是解答本题的关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
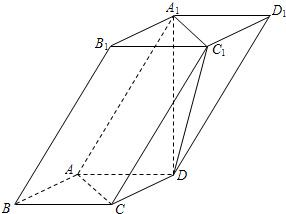 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.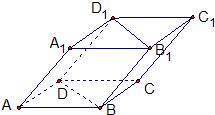 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是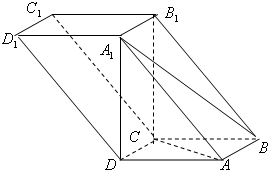 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,