题目内容
已知f（x）是定义在R上的函数且f（x）=
，若f（0）=2+
，则f（2008）等于 ．
| 1+f(x-2) |
| 1-f(x-2) |
| 3 |
考点：抽象函数及其应用,函数的值
专题：函数的性质及应用
分析：根据题意通过f（x）=
，推出函数的周期，再结合题意即可得到答案．
| 1+f(x-2) |
| 1-f(x-2) |
解答：
解：因为f（0）=2+
，f（x）=
，
所以f（x+2）=
=
=-
，
所以f（x+8）=-
=f（x），
所以f（x）是定义在实数集上周期为8的函数，
所以f（2008）=f（0）=2+
，
故答案为：2+
．
| 3 |
| 1+f(x-2) |
| 1-f(x-2) |
所以f（x+2）=
| 1+f(x) |
| 1-f(x) |
1+
| ||
1-
|
| 1 |
| f(x-2) |
所以f（x+8）=-
| 1 |
| f(x+4) |
所以f（x）是定义在实数集上周期为8的函数，
所以f（2008）=f（0）=2+
| 3 |
故答案为：2+
| 3 |
点评：本题主要考查利用抽象函数求出函数的周期，函数值的求法，像这种计算较大自变量的函数值时一般先根据题意求出函数的周期，再利用周期的有关性质进行解题．
练习册系列答案
相关题目
已知f（x）=2012x+
+2014，α，β表示锐角三角形的两个内角，则下列结论正确的是（ ）
| 2013 |
| x |
| A、f（cosα）＞f（cosβ） |
| B、f（sinα）＞f（sinβ） |
| C、f（sinα）＞f（cosβ） |
| D、f（sinα）＜f（cosβ） |
如图所示，A，B，C，D是圆O上的四个点，DE为圆O的切线，AC∥DE，直线AC与BD交于点F，若AB=2，AD=3，BD=4，则CF=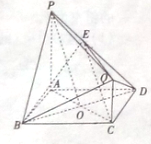
如图，直线PA，QC都与正方形ABCD所在平面垂直，AB=PA=2QC=2，AC与BD相交于点O，E在线段PD上且CE∥平面PBQ