题目内容
10．已知函数f（x）满足f（x+3）=$\frac{1}{f（x）}$，且f（-2）=2，则f（2017）=$\frac{1}{2}$．分析 由已知得f（x+6）=$\frac{1}{f（x+3）}$=f（x），从而f（2017）=f（336×6+1）=f（1）=f（-2+3）=$\frac{1}{f（-2）}$，由此能求出结果．
解答 解：∵函数f（x）满足f（x+3）=$\frac{1}{f（x）}$，
∴f（x+6）=$\frac{1}{f（x+3）}$=f（x），
∵f（-2）=2，
∴f（2017）=f（336×6+1）=f（1）=f（-2+3）=$\frac{1}{f（-2）}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数的周期性的合理运用．
练习册系列答案
相关题目
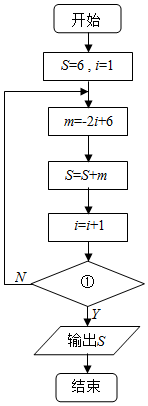如果图中所示的流程图的输出结果为-18，那么在判断框①中用i表示的“条件”应该是i＞8？．
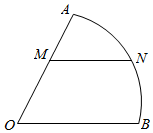如图，扇形AOB是某个旅游景点的平面示意图，圆心角AOB的大小等于$\frac{π}{3}$，半径OA=200m，点M在半径OA上，点N在$\widehat{AB}$上，且MN∥OB，求观光道路OM与MN长度之和的最大值．