题目内容
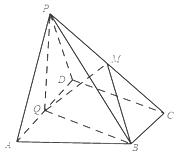
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC= 
AD=1，CD= 
． 
（1）求证：平面MQB⊥平面PAD；
（2）若二面角M﹣BQ﹣C大小的为60°，求QM的长．
【答案】
（1）解：∵AD∥BC，BC= 
AD，Q为AD的中点，
∴四边形BCDQ为平行四边形，∴CD∥BQ
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD．
又∵平面PAD⊥平面ABCD且平面PAD∩平面ABCD=AD，
∴BQ⊥平面PAD．∵BQ平面MQB，∴平面MQB⊥平面PAD
（2）解：∵PA=PD，Q为AD的中点，∴PQ⊥AD．
∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PQ⊥平面ABCD．
如图，以Q为原点建立空间直角坐标系．
则Q（0，0，0），A（1，0，0），P（0，0， 
），B（0， ，0），C（﹣1， ，0），
由 
= 
= 
，且0≤λ≤1，得M（ 
）
所以 
=（ 
），又 
=（0， ，0），
∴平面MBQ法向量为 
=（ 
）
由题意知平面BQC的法向量为 
=（0，0，1）
∵二面角M﹣BQ﹣C为60°，
∴cos60°= 
= ，∴ 
∴|QM|= 
【解析】（1）证明CD∥BQ，推出QB⊥AD．得到BQ⊥平面PAD，然后证明平面MQB⊥平面PAD．（2）证明PQ⊥AD．推出PQ⊥平面ABCD，以Q为原点建立空间直角坐标系．求出相关点的坐标，求出平面MBQ法向量，平面BQC的法向量，然后利用利用空间向量的数量积求解即可．
【考点精析】根据题目的已知条件，利用平面与平面垂直的判定的相关知识可以得到问题的答案，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直．
