题目内容
如图,已知直四棱柱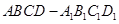 的底面是直角梯形,
的底面是直角梯形,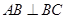 ,
,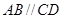 ,
, ,
,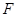 分别是棱
分别是棱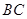 ,
,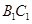 上的动点,且
上的动点,且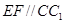 ,
,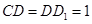 ,
,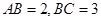 .
.
(Ⅰ)证明:无论点 怎样运动,四边形
怎样运动,四边形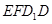 都为矩形;
都为矩形;
(Ⅱ)当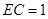 时,求几何体
时,求几何体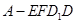 的体积。
的体积。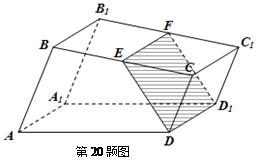
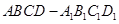 的底面是直角梯形,
的底面是直角梯形,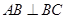 ,
,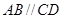 ,
, ,
,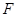 分别是棱
分别是棱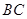 ,
,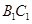 上的动点,且
上的动点,且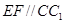 ,
,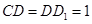 ,
,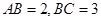 .
.(Ⅰ)证明:无论点
 怎样运动,四边形
怎样运动,四边形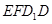 都为矩形;
都为矩形;(Ⅱ)当
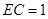 时,求几何体
时,求几何体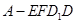 的体积。
的体积。
(Ⅰ)在直四棱柱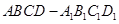 中,
中,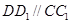 ,
,
∵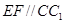 ,∴
,∴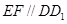 , ---------------------------------------2分
, ---------------------------------------2分
又∵平面 平面
平面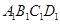 ,平面
,平面 平面
平面 ,
,
平面 平面
平面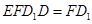 ,
,
∴ ,∴四边形
,∴四边形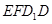 为平行四边形,-----------------4分
为平行四边形,-----------------4分
∵侧棱 底面
底面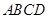 ,又
,又 平面
平面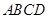 内,
内,
∴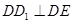 ,∴四边形
,∴四边形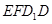 为矩形; -----------------------------5分
为矩形; -----------------------------5分
(Ⅱ)证明:连结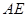 ,∵四棱柱
,∵四棱柱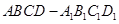 为直四棱柱,
为直四棱柱,
∴侧棱 底面
底面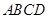 ,又
,又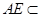 平面
平面 内,∴
内,∴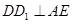 , -------6分
, -------6分
在 中,
中,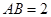 ,
, ,则
,则 ; ---------------7分
; ---------------7分
在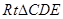 中,
中,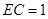 ,
,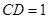 ,则
,则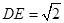 ; -------------8分
; -------------8分
在直角梯形中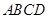 ,
,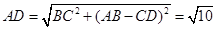 ;
;
∴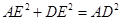 ,即
,即 ,
,
又∵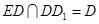 ,∴
,∴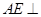 平面
平面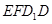 ; ---------------10分
; ---------------10分
由(Ⅰ)可知,四边形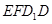 为矩形,且
为矩形,且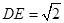 ,
, ,
,
∴矩形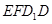 的面积为
的面积为 ,
,
∴几何体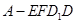 的体积为
的体积为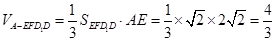
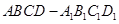 中,
中,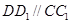 ,
,∵
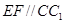 ,∴
,∴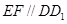 , ---------------------------------------2分
, ---------------------------------------2分又∵平面
 平面
平面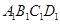 ,平面
,平面 平面
平面 ,
,平面
 平面
平面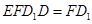 ,
,∴
 ,∴四边形
,∴四边形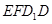 为平行四边形,-----------------4分
为平行四边形,-----------------4分∵侧棱
 底面
底面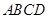 ,又
,又 平面
平面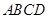 内,
内,∴
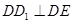 ,∴四边形
,∴四边形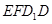 为矩形; -----------------------------5分
为矩形; -----------------------------5分(Ⅱ)证明:连结
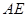 ,∵四棱柱
,∵四棱柱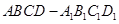 为直四棱柱,
为直四棱柱,∴侧棱
 底面
底面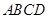 ,又
,又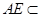 平面
平面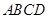 内,∴
内,∴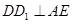 , -------6分
, -------6分在
 中,
中,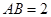 ,
, ,则
,则 ; ---------------7分
; ---------------7分在
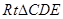 中,
中,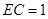 ,
,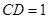 ,则
,则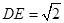 ; -------------8分
; -------------8分在直角梯形中
 ,
,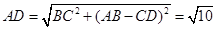 ;
;∴
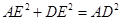 ,即
,即 ,
,又∵
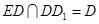 ,∴
,∴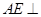 平面
平面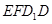 ; ---------------10分
; ---------------10分由(Ⅰ)可知,四边形
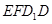 为矩形,且
为矩形,且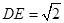 ,
, ,
,∴矩形
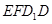 的面积为
的面积为 ,
,∴几何体
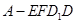 的体积为
的体积为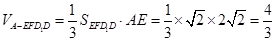
略

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
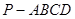 中,
中,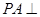 平面
平面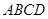 ,底面
,底面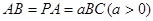 .
.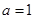 时,求证:
时,求证: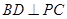 ;
;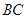 边上有且只有一个点
边上有且只有一个点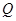 ,使得
,使得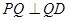 ,求此时二面角
,求此时二面角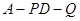 的余弦值.
的余弦值.
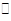 平面
平面 ,点P
,点P
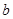 、
、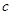 表示两条直线,
表示两条直线,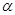 、
、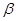 表示两个平面,下列命题中真命题是( )
表示两个平面,下列命题中真命题是( )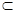
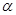 ,
,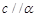 则
则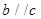 ,
, ,则
,则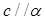
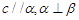 ,则
,则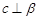
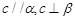 ,则
,则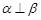
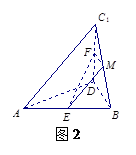
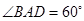 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线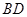 翻折,使点
翻折,使点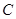 翻折到点
翻折到点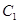 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.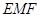 ;
;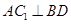 ;
;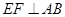 时,求线段AC1的长.
时,求线段AC1的长.
 中,若点
中,若点 (异于点
(异于点 )是棱上一点,则满足
)是棱上一点,则满足 与
与 所成的角为
所成的角为 的点
的点
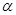 ,
,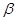 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )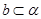 时,若b⊥
时,若b⊥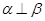
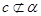 时,若c∥
时,若c∥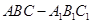 中,
中, ,
, ,点
,点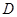 在
在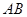 上.
上.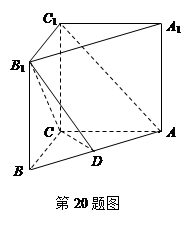
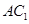 ∥平面
∥平面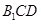 ;
;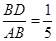 时,求二面角
时,求二面角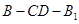 的余弦值.
的余弦值.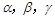 满足
满足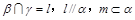 ,
, ,则有
,则有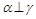 且
且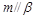
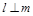
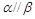 且
且