题目内容
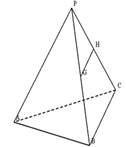
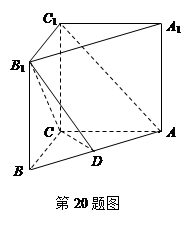
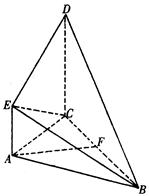
(本小题满分12分)已知直三棱柱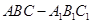 中,
中, ,
, ,点
,点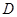 在
在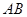 上.
上.
(1)若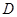 是
是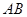 中点,求证:
中点,求证: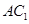 ∥平面
∥平面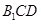 ;
;
(2)当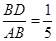 时,求二面角
时,求二面角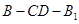 的余弦值.
的余弦值.
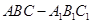 中,
中, ,
, ,点
,点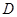 在
在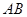 上.
上.
(1)若
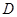 是
是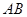 中点,求证:
中点,求证: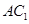 ∥平面
∥平面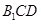 ;
;(2)当
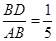 时,求二面角
时,求二面角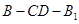 的余弦值.
的余弦值.(1)证明:连结BC1,交B1C于E,DE.
∵ 直三棱柱ABC-A1B1C1,D是AB中点,
∴侧面B B1C1C为矩形,DE为△ABC1的中位线,
∴ DE// AC1. …………………………………2分
因为 ∵DE 平面B1CD, AC1
平面B1CD, AC1 平面B1CD,
平面B1CD,
∴AC1∥平面B1CD. …………………………………4分
(2) ∵ AC⊥BC,
所以如图,以C为原点建立空间直角坐标系C-xyz.

则B (3, 0, 0),A (0, 4, 0),A1 (0, 0, c),B1 (3, 0, 4).
设D (a, b, 0)(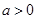 ,
,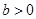 ), …………………5分
), …………………5分
∵点D在线段AB上,且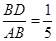 , 即
, 即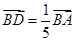 .
.
∴ . …………………7分
. …………………7分
所以 ,
,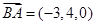 ,
, .
.
高三数学(理工类)参考答案第2页(共4页)
平面BCD的法向量为.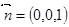 ……………………………………8分
……………………………………8分
设平面B1 CD的法向量为 ,
,
由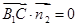 ,
,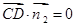 , 得
, 得 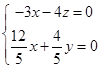 ,
,
所以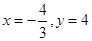 ,
,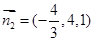 . ……………………………………10分
. ……………………………………10分
设二面角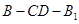 的大小为
的大小为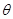 ,
, 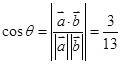 . ……………………11分
. ……………………11分
所以二面角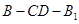 的余弦值为
的余弦值为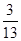 . ……………………12分
. ……………………12分
∵ 直三棱柱ABC-A1B1C1,D是AB中点,
∴侧面B B1C1C为矩形,DE为△ABC1的中位线,
∴ DE// AC1. …………………………………2分
因为 ∵DE
 平面B1CD, AC1
平面B1CD, AC1 平面B1CD,
平面B1CD, ∴AC1∥平面B1CD. …………………………………4分
(2) ∵ AC⊥BC,
所以如图,以C为原点建立空间直角坐标系C-xyz.

则B (3, 0, 0),A (0, 4, 0),A1 (0, 0, c),B1 (3, 0, 4).
设D (a, b, 0)(
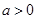 ,
,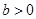 ), …………………5分
), …………………5分∵点D在线段AB上,且
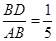 , 即
, 即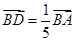 .
.∴
 . …………………7分
. …………………7分所以
 ,
,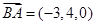 ,
, .
. 高三数学(理工类)参考答案第2页(共4页)
平面BCD的法向量为.
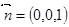 ……………………………………8分
……………………………………8分设平面B1 CD的法向量为
 ,
,由
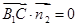 ,
,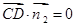 , 得
, 得 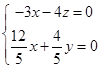 ,
, 所以
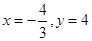 ,
,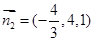 . ……………………………………10分
. ……………………………………10分 设二面角
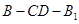 的大小为
的大小为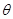 ,
, 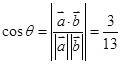 . ……………………11分
. ……………………11分所以二面角
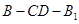 的余弦值为
的余弦值为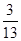 . ……………………12分
. ……………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
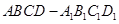 的底面是直角梯形,
的底面是直角梯形,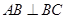 ,
,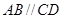 ,
, ,
,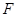 分别是棱
分别是棱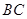 ,
,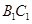 上的动点,且
上的动点,且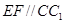 ,
,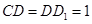 ,
,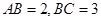 .
.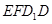 都为矩形;
都为矩形;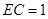 时,求几何体
时,求几何体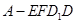 的体积。
的体积。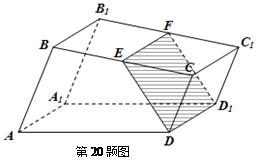
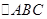 所在平面互相垂直,F为BC的中点,
所在平面互相垂直,F为BC的中点,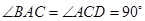 ,AE∥CD,
,AE∥CD,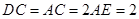 .
.
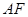 ∥平面
∥平面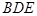 ;
;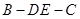 的余弦值.
的余弦值.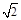 ,AB=1,E是DD1的中点。
,AB=1,E是DD1的中点。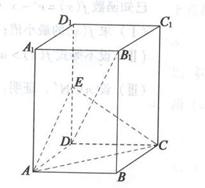
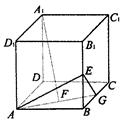
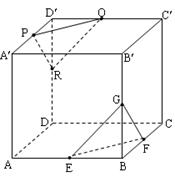
 中,E、F、G分别是
中,E、F、G分别是 、AB、BC的中点.
、AB、BC的中点.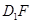 ⊥平面AEG;
⊥平面AEG;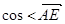 ,
,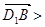
 与
与 互相平行的一个充分条件是
互相平行的一个充分条件是 都平行于同一平面
都平行于同一平面