题目内容
14.过点M(1,1)的直线与双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$交于A,B两点,且点M平分AB,则直线AB的方程为( )| A. | 4x+3y-7=0 | B. | 3x+4y+1=0 | C. | 3x-4y-7=0 | D. | 4y-3x-1=0 |
分析 利用点差法及中点坐标公式,求得得直线AB的斜率,根据直线的点斜式方程即可求得直线AB的方程.
解答 解:设A(x1,y1),B(x2,y2),
代入椭圆的方程可得:$\frac{{x}_{1}^{2}}{4}-\frac{{y}_{1}^{2}}{3}=1$,$\frac{{x}_{2}^{2}}{4}-\frac{{y}_{2}^{2}}{3}=1$,
两式相减可得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$=$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{3}$,
由中点坐标公式可知:x1+x2=2,y1+y2=2,
由直线k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{3}{4}$,
则直线AB的方程为:y-1=$\frac{3}{4}$(x-1),化为4y-3x-1=0.
故选:D.
点评 本题考查直线方程的求法,考查点差法的应用,考查计算能力,属于中档题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
9.数列{an},{bn}为等差数列,前n项和分别为Sn,Tn,若$\frac{S_n}{T_n}=\frac{3n+2}{2n}$,则$\frac{a_7}{b_7}$=( )
| A. | $\frac{41}{26}$ | B. | $\frac{23}{14}$ | C. | $\frac{11}{7}$ | D. | $\frac{11}{6}$ |
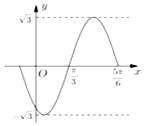 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )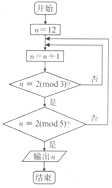 若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )
若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=4(mod7),如图所示的程序框图的算法源于我国古代闻名中外的《中国剩余定理》,执行该程序框图,则输出的n=( )