题目内容
5.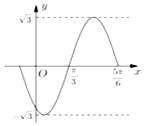 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )①函数f(x)的最小正周期为$\frac{π}{2}$
②函数f(x)的振幅为$2\sqrt{3}$
③函数f(x)的一条对称轴方程为$x=\frac{7π}{12}$
④函数f(x)的单调递增区间是$[{\frac{π}{12},\frac{7π}{12}}]$
⑤函数f(x)的解析式为$f(x)=\sqrt{3}sin({2x-\frac{2π}{3}})$.
| A. | ③⑤ | B. | ③④ | C. | ④⑤ | D. | ①③ |
分析 根据图象求出函数解析式,根据三角函数型函数的性质逐一判定.
解答 解:由图象可知T=2($\frac{5π}{6}-\frac{π}{3})=π$,∴ω=2,最大值为$\sqrt{3}$,∴$A=\sqrt{3}$,$f(x)=\sqrt{3}sin(2x+$φ)
因为图象过点($\frac{π}{3},0$),2×$\frac{π}{3}$+φ=π,⇒φ=-$\frac{2π}{3}$,∴$f(x)=\sqrt{3}sin(2x-\frac{2π}{3})$
即可判定①②错,⑤正确,
由2x-$\frac{2π}{3}$=kπ+$\frac{π}{2}$得对称轴方程为x=$\frac{kπ}{2}+\frac{7π}{12}$,k∈Z,故③正确;
由2kπ-$\frac{π}{2}$2x-$\frac{2π}{3}$$≤2kπ+\frac{π}{2}$,⇒kπ+$\frac{π}{12}$≤x$≤kπ+\frac{7π}{12}$,k∈Z,
函数f(x)的单调递增区间是[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],故④错;
故选:A
点评 本题考查了根据图象求三角函数型函数的解析式,及三角函数型函数的性质,属于基础题.

练习册系列答案
相关题目
16.某地天气预报说:“明天本地降雨的概率为80%”,这是指( )
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
20.等比数列{an}中,a1>1,前n项和为Sn,若$\lim_{x→∞}{S_n}=\frac{1}{a_1}$,那么a1的取值范围是( )
| A. | (1,+∞) | B. | (1,2) | C. | $(1\;,\;\;\sqrt{3})$ | D. | $(1\;,\;\;\sqrt{2})$ |
10.已知点O为△ABC所在平面内一点,${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$,若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,且$|{\overrightarrow{AC}}|=|{\overrightarrow{AO}}|$,则$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
17.已知函数f(x)=2sin(ωx+φ)+1(ω>0,|φ|≤$\frac{π}{2}}$),其图象与直线y=2最近的两个相邻交点间的距离为$\frac{π}{3}$,若f(x)>1对$?x∈({-\frac{π}{8},\frac{π}{3}})$恒成立,则φ的取值范围是( )
| A. | $[{\frac{π}{4},\frac{π}{3}}]$ | B. | $[{-\frac{π}{6},\frac{π}{4}}]$ | C. | $[{\frac{π}{6},\frac{π}{4}}]$ | D. | $({\frac{π}{6},\frac{π}{2}}]$ |
14.过点M(1,1)的直线与双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$交于A,B两点,且点M平分AB,则直线AB的方程为( )
| A. | 4x+3y-7=0 | B. | 3x+4y+1=0 | C. | 3x-4y-7=0 | D. | 4y-3x-1=0 |
15.将一枚均匀硬币先后抛两次,恰好有一次出现正面的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |