题目内容
在平面直角坐标系中,曲线C1:x2+y2=1,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线l:3cosθ-2sinθ=
(Ⅰ)将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的2倍、3倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程;
(Ⅱ)求C2上一点P到l的距离的最大值.
| -8 |
| ρ |
(Ⅰ)将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的2倍、3倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程;
(Ⅱ)求C2上一点P到l的距离的最大值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(Ⅰ)直线l:3cosθ-2sinθ=
化为3ρcosθ-2ρsinθ=-8,把x=ρcosθ,y=ρsinθ代入就看得出直线l的直角坐标方程.由题意得曲线C2的直角坐标方程为
+
=1,即可得出曲线C2的参数方程为
(θ为参数).
(Ⅱ) 设点P的坐标为(2cosθ,3sinθ),则点P到直线l的距离为d=
=
,再利用余弦函数的单调性即可得出.
| -8 |
| ρ |
| x2 |
| 4 |
| y2 |
| 9 |
|
(Ⅱ) 设点P的坐标为(2cosθ,3sinθ),则点P到直线l的距离为d=
| |6cosθ-6sinθ+8| | ||
|
|6
| ||||
|
解答:
解:(Ⅰ) 由题意知,直线l的直角坐标方程为3x-2y+8=0.
由题意得曲线C2的直角坐标方程为
+
=1,
∴曲线C2的参数方程为
(θ为参数).
(Ⅱ) 设点P的坐标为(2cosθ,3sinθ),
则点P到直线l的距离为d=
=
,
∴当cos(θ+
)=1时,dmax=
.
由题意得曲线C2的直角坐标方程为
| x2 |
| 4 |
| y2 |
| 9 |
∴曲线C2的参数方程为
|
(Ⅱ) 设点P的坐标为(2cosθ,3sinθ),
则点P到直线l的距离为d=
| |6cosθ-6sinθ+8| | ||
|
|6
| ||||
|
∴当cos(θ+
| π |
| 4 |
6
| ||||
| 13 |
点评:本题考查了极坐标方程化为直角坐标方程、椭圆的参数方程、点到直线的距离公式、余弦函数的单调性,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
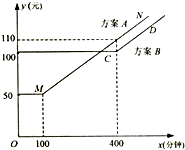 移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).
移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等). 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.