题目内容
14.已知函数f(x)是定义在[a-a2,a+3](a>0)的偶函数,且当x≥0时单调递增,f(1)=0,则f(lnx)>0的解集为[e-6,e-1)∪(e,e6].分析 根据函数奇偶性的性质利用定义域关于原点对称求出a的值,结合函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:∵函数是偶函数,∴定义域关于原点对称,
则a-a2+a+3=0,
即a2-2a-3=0,即a=3或a=-1(舍),
即函数的定义域为[-6,6],
∵当x≥0时单调递增,f(1)=0,
∴f(lnx)>0等价为f(lnx)>f(1),
即f(|lnx|)>f(1),
则1<|lnx|≤6,
即-6≤lnx<-1或1<lnx≤6,
得e-6≤x<e-1或e<x≤e6,
故答案为:[e-6,e-1)∪(e,e6]
点评 本题主要考查不等式的求解,根据函数奇偶性的定义和性质将不等式进行转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在△ABC中,若tanB=$\frac{cos(C-B)}{sinA+sin(C-B)}$,则这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰三角形或直角三角形 |
6.以初速40m/s竖直向上抛一物体,t s时刻的速度v=40-10t,则此物体达到最高时的高度为( )
| A. | 160m | B. | 80m | C. | 40m | D. | 20m |
2.某单位有老年人28人,中年人56人,青年人84人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36的样本,则老年人、中年人、青年人分别抽取的人数是( )
| A. | 6,12,18 | B. | 7,11,19 | C. | 6,13,17 | D. | 7,12,17 |
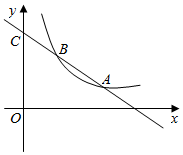 如图函数y1=k1x+b的图象与函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象交于A、B两点,与y轴交于c点.已知A点的坐标为(2,1).c点坐标为(0.3).
如图函数y1=k1x+b的图象与函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象交于A、B两点,与y轴交于c点.已知A点的坐标为(2,1).c点坐标为(0.3).