题目内容
2．某单位有老年人28人，中年人56人，青年人84人，为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为36的样本，则老年人、中年人、青年人分别抽取的人数是（ ）| A． | 6，12，18 | B． | 7，11，19 | C． | 6，13，17 | D． | 7，12，17 |
分析 利用分层抽样，先求出抽样比，再计算老年人、中年人、青年人分别各抽取的人数．
解答 解：∵单位有老年人28人，中年人56人，青年人84人，
为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为36样本，每个人被抽到的概率为$\frac{36}{28+56+84}$=$\frac{3}{14}$
∴利用分层抽样方法得到：
老年人应抽取的人数为：$\frac{3}{14}$×28=6人，
中年人应抽取的人数为：$\frac{3}{14}$×56=12人，
青年人应抽取的人数为：$\frac{3}{14}$×84=18人．
故选：A．
点评 本题考查分层抽样的应用，是基础题，解题时要注意分层抽样的性质的合理运用．
练习册系列答案
相关题目
13．已知二次方程ax2+bx+c=0的根为2，4且a＞0，则ax2+bx+c＞0的解集是（ ）
| A． | {x|2＜x＜4} | B． | {x|x＜2或x＞4} | C． | {x|4＜x＜2} | D． | {x|x＜4或x＞2} |
14．要得到函数$y=sin（{\frac{1}{2}x-\frac{π}{3}}）$的图象，只要将函数$y=cos\frac{1}{2}x$的图象（ ）
| A． | 向左平行移动$\frac{5π}{3}$个单位 | B． | 向左平行移动$\frac{5π}{6}$个单位 | ||
| C． | 向右平行移动$\frac{5π}{3}$个单位 | D． | 向右平行移动$\frac{5π}{6}$个单位 |
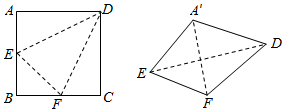如图，边长为2的正方形ABCD中，点E、F分别是AB、BC的中点，将△ADE、△EBF、△FCD分别沿DE、EF、FD折起，使得A、B、C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的半径为$\frac{\sqrt{6}}{2}$．