题目内容
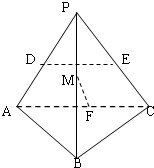如图所示，正三棱锥P-ABC中，D．E、F分别为PA．PC．AC的中点，M为PB上的任意一点，则DE与MF所成角的大小为（ ）| A、30° | B、60° |
| C、90° | D、随点M变化而变化 |
考点：异面直线及其所成的角
专题：空间角
分析：连结PF，BF，则PF⊥AC，BF⊥AC，DE∥AC，从而AC⊥平面BPF，由此能求出DE与MF所成角的大小为90°．
解答：
解：连结PF，BF，
∵正三棱锥P-ABC中，D．E、F分别为PA．PC．AC的中点，
∴PF⊥AC，BF⊥AC，DE∥AC，
又PF∩BF=F，
∴AC⊥平面BPF，
又MF?平面BPF，
∴AC⊥MF，
∵DE∥AC，∴DE⊥MF．
∴DE与MF所成角的大小为90°．
故选：C．
解：连结PF，BF，∵正三棱锥P-ABC中，D．E、F分别为PA．PC．AC的中点，
∴PF⊥AC，BF⊥AC，DE∥AC，
又PF∩BF=F，
∴AC⊥平面BPF，
又MF?平面BPF，
∴AC⊥MF，
∵DE∥AC，∴DE⊥MF．
∴DE与MF所成角的大小为90°．
故选：C．
点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
复数z=1+
的虚部为（ ）
| 1 |
| i |
| A、1 | B、i | C、-1 | D、-i |
设R表示实数集，A=[-1，2]，B=（0，+∞），则A∩∁RB等于（ ）
| A、（0，2] |
| B、（-∞，2] |
| C、（-1，+∞） |
| D、[-1，0] |
如图所示，AC1是正方体的一条体对角线，点P，Q分别为其在棱的中点，则PQ与AC1所成的角为（ ）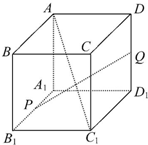 
A、
| ||
B、
| ||
C、
| ||
D、
|
