题目内容
5.已知函数f(x)满足f(x)=x3+ax2-x+c(c>0),且$a=f'(\frac{2}{3})$(Ⅰ)求a的值;
(Ⅱ)若方程f(x)=0有且只有两个不等的实根,求常数c;
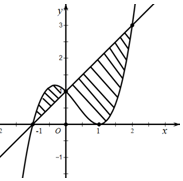
(Ⅲ)在(Ⅱ)的条件下,求曲线f(x)与直线g(x)=x+1围成封闭图形的面积.
分析 (Ⅰ)先求导,再代值计算即可;
(Ⅱ)当$f(-\frac{1}{3})=0$或f(1)=0时,f(x)=0有且只有两个不等的实根,即可求出c的值,
(Ⅲ)根据定积分在几何中的应用即可求出
解答 (Ⅰ)解:∵f(x)=x3+ax2-x+c,f'(x)=3x2+2ax-1,
令$x=\frac{2}{3}$得:$f'(\frac{2}{3})=3{(\frac{2}{3})^2}+2f'(\frac{2}{3})•\frac{2}{3}-1$,解得$f'(\frac{2}{3})=-1$,
即a=-1先判断函数的单调性,再根据
(Ⅱ)由f(x)=x3-x2-x+c得f'(x)=3x2-2x-1=(3x+1)(x-1)
| x | $({-∞,-\frac{1}{3}})$ | $-\frac{1}{3}$ | $(-\frac{1}{3},1)$ | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
即$c+\frac{5}{27}=0$或c-1=0,
∵c>0,
∴c=1,
(Ⅲ)由f(x)=g(x)得,x3-x2-x+1=x+1,
解得:x=-1,0,2
所以曲线f(x)与直线g(x)=x+1围成封闭图形的面积$S=\int_{-1}^0{({x^3}-{x^2}-2x)}dx-\int_0^2{({x^3}-{x^2}-2x)}dx=\frac{37}{12}$.
点评 本题考查了导数和函数的单调性以及方程根的问题,考查了定积分的应用,属于中档题

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
15.世界最大单口径射电望远镜FAST于2016年9月25日在贵州省黔南州落成启用,它被誉为“中国天眼”,从选址到启用历经22年.FAST选址从开始一万多个地方逐一审查,最后敲定三个地方:贵州省黔南州、黔西南州和安顺市境内.现从这三个地方中任选两个地方重点研究其条件状况,则贵州省黔南州被选中的概率为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
 某市随机抽取部分企业调查年上缴税收情况{单位万元,将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100]样本数据分组为[0,20),[20,40)[40,60)[60,80),[80,100)
某市随机抽取部分企业调查年上缴税收情况{单位万元,将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100]样本数据分组为[0,20),[20,40)[40,60)[60,80),[80,100)