Question

【题目】如图所示，在四边形ABCD中，AB⊥DA，CE= ，∠ADC= ；E为AD边上一点，DE=1，EA=2，∠BEC=

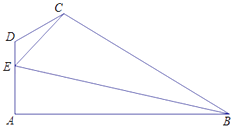
（1）求sin∠CED的值；
（2）求BE的长．

Answer 1

【答案】
（1）解：设∠CED=α．在△CED中，由余弦定理，得

CE2=CD2+DE2﹣2CD×DE×cos∠CDE，

得CD2+CD﹣6=0，解得CD=2（CD=﹣3舍去）．

在△CED中，由正弦定理，得sin∠CED= ．

（2）解：由题设知α∈（0， ），所以cos ，

而∠AEB= ，

所以cos∠AEB=cos（ ）

=cos cosα+sin sinα

=﹣ cosα+ sinα

=﹣

= ．

在Rt△EAB中，BE= =4 ．

【解析】（1）设∠CED=α．在△CED中，由余弦定理，可解得CD=2，在△CED中，由正弦定理可解得sin∠CED的值．（2）由题设知α∈（0， ），先求cos ，而∠AEB= ，即可求cos∠AEB=cos（ ）的值．
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本，需要知道正弦定理:；余弦定理:;;．