题目内容
【题目】已知函数f(x)=asin(2ωx+ ![]() )+
)+ ![]() +b(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是
+b(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是 ![]() ,最小值是
,最小值是 ![]() .
.
(1)求ω、a、b的值;
(2)求f(x)的单调递增区间.
【答案】
(1)解:由函数f(x)=asin(2ωx+ ![]() )+
)+ ![]() +b的最小正周期为π,
+b的最小正周期为π,
得 ![]() =π,∴ω=1,
=π,∴ω=1,
又f(x)的最大值是 ![]() ,最小值是
,最小值是 ![]() ,
,
则 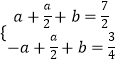 ,
,
解得 ![]() ;
;
(2)解:由(1)知,f(x)= ![]() sin(2x+
sin(2x+ ![]() )+
)+ ![]() ,
,
当2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() (k∈Z),
(k∈Z),
即kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() (k∈Z)时,f(x)单调递增,
(k∈Z)时,f(x)单调递增,
∴f(x)的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
【解析】(1)由函数f(x)的最小正周期求出ω的值,再由f(x)的最值求出a、b的值;(2)根据正弦函数的图象与性质,令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() (k∈Z),即可求出f(x)的单调增区间.
(k∈Z),即可求出f(x)的单调增区间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为
之间是正相关还是负相关;若该地1月份某天的最低气温为![]() ,请用所求回归方程预测该店当日的销售量;
,请用所求回归方程预测该店当日的销售量;
(3)设该地1月份的日最低气温![]() ~
~![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() ,求
,求![]() .
.
附:①回归方程![]() 中,
中, 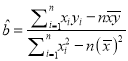 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,则
,则![]() ,
, ![]() .
.