题目内容
已知中心在原点,焦点在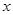 轴上的椭圆,离心率
轴上的椭圆,离心率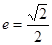 ,且经过抛物线
,且经过抛物线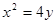 的焦点.
的焦点.
(1)求椭圆的标准方程;
(2)若过点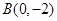 的直线
的直线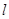 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点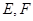 (
(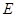 在
在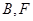
之间),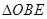 与
与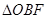 面积之比为
面积之比为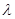 ,求
,求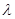 的取值范围.
的取值范围.
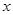 轴上的椭圆,离心率
轴上的椭圆,离心率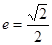 ,且经过抛物线
,且经过抛物线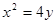 的焦点.
的焦点.(1)求椭圆的标准方程;
(2)若过点
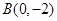 的直线
的直线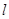 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点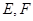 (
(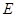 在
在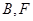
之间),
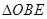 与
与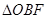 面积之比为
面积之比为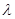 ,求
,求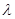 的取值范围.
的取值范围.解:(1)设椭圆的方程为 ,则
,则 ①,
①,
∵抛物线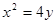 的焦点为(0, 1), ….2分
的焦点为(0, 1), ….2分
∴ ②
②
由①②解得 . ……4分
. ……4分
∴椭圆的标准方程为 . ……5分
. ……5分
(2)如图,由题意知 的斜率存在且不为零,
的斜率存在且不为零,

设 方程为
方程为 ③,
③,
将③代入 ,整理,得
,整理,得
 ,由
,由 得
得 ……7分
……7分
设 、
、 ,则
,则 ④
④
令 , 则
, 则 ,……9分
,……9分
由此可得 ,
, ,且
,且 .由④知
.由④知  ,
, .
.
∴ , 即
, 即 ……12分
……12分
∵ ,∴
,∴  ,解得
,解得
又∵ , ∴
, ∴ ,……13分
,……13分
∴ OBE与
OBE与 OBF面积之比的取值范围是(
OBF面积之比的取值范围是( , 1). ……14分
, 1). ……14分
 ,则
,则 ①,
①,∵抛物线
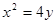 的焦点为(0, 1), ….2分
的焦点为(0, 1), ….2分 ∴
 ②
②由①②解得
 . ……4分
. ……4分∴椭圆的标准方程为
 . ……5分
. ……5分 (2)如图,由题意知
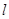 的斜率存在且不为零,
的斜率存在且不为零,
设
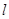 方程为
方程为 ③,
③,将③代入
 ,整理,得
,整理,得 ,由
,由 得
得 ……7分
……7分设
 、
、 ,则
,则 ④
④令
 , 则
, 则 ,……9分
,……9分由此可得
 ,
, ,且
,且 .由④知
.由④知  ,
, .
.∴
 , 即
, 即 ……12分
……12分∵
 ,∴
,∴  ,解得
,解得
又∵
 , ∴
, ∴ ,……13分
,……13分∴
 OBE与
OBE与 OBF面积之比的取值范围是(
OBF面积之比的取值范围是( , 1). ……14分
, 1). ……14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
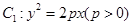 的焦点
的焦点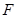 以及椭圆
以及椭圆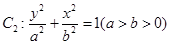 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆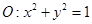 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程;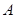 、
、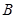 两不同点,交
两不同点,交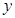 轴于点
轴于点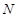 ,已知
,已知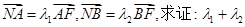 为定值.
为定值.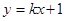 ,当
,当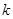 变化时,直线被椭圆
变化时,直线被椭圆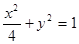 截得的最大弦长是( )
截得的最大弦长是( )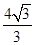
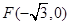 ,右顶点为
,右顶点为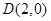 ,设点
,设点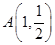 .(1)求该椭圆的标准方程;
.(1)求该椭圆的标准方程;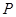 是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点
是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点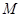 的轨迹方程;
的轨迹方程; 点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,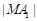 ∶
∶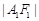 = 2∶1.
= 2∶1.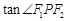 的最大值.
的最大值.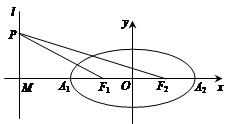
 的离心率
的离心率 ,则
,则 的值为
的值为
 或
或

 或
或 相交所得的弦恰好被P平分,则此椭圆的离心率是 ;
相交所得的弦恰好被P平分,则此椭圆的离心率是 ; 的直线
的直线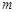 与椭圆
与椭圆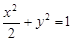 交于
交于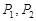 ,线段
,线段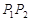 的中点为
的中点为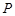 ,设直线
,设直线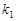 ,直线
,直线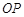 的斜率为
的斜率为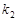 ,则
,则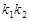 的值为
的值为 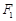 、
、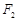 是椭圆C:
是椭圆C: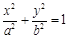 (
(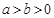 )的两个焦点,P为椭圆C上的一点,且
)的两个焦点,P为椭圆C上的一点,且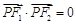 。若
。若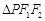 的面积为9,则
的面积为9,则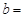 _________。
_________。