题目内容
9.已知a、b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=5,ab=2.分析 a、b∈R,(a+bi)2=3+4i(i是虚数单位),可得3+4i=a2-b2+2abi,可得3=a2-b2,2ab=4,解出即可得出.
解答 解:a、b∈R,(a+bi)2=3+4i(i是虚数单位),
∴3+4i=a2-b2+2abi,
∴3=a2-b2,2ab=4,
解得ab=2,$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,$\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$.
则a2+b2=5,
故答案为:5,2.
点评 本题考查了复数的运算法则、复数的相等、方程的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的离心率是( )
| A. | $\frac{\sqrt{13}}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
14.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别是x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
| A. | x1,x2,…,xn的平均数 | B. | x1,x2,…,xn的标准差 | ||
| C. | x1,x2,…,xn的最大值 | D. | x1,x2,…,xn的中位数 |
1.设复数z满足(1+i)z=2i,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
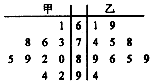 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.