题目内容
对于定义域为D的函数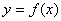 ,若同时满足下列条件:①
,若同时满足下列条件:①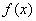 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[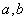 ]
]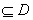 ,使
,使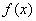 在[
在[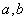 ]上的值域为[
]上的值域为[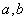 ];那么把
];那么把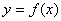 (
(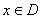 )叫闭函数。
)叫闭函数。
(Ⅰ)求闭函数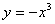 符合条件②的区间[
符合条件②的区间[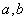 ];(Ⅱ)判断函数
];(Ⅱ)判断函数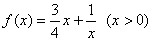 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(Ⅲ)若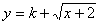 是闭函数,求实数
是闭函数,求实数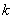 的取值范围。
的取值范围。
解:(Ⅰ)由题意,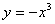 在[
在[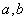 ]上递减, 则
]上递减, 则 解得
解得 所以,所求的区间为[-1,1] (Ⅱ)
所以,所求的区间为[-1,1] (Ⅱ)
解:取 则
则 ,即
,即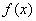 不是
不是 上的减函数。…………6分
上的减函数。…………6分
取
 , 即
, 即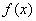 不是
不是 上的增函数 所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。 (Ⅲ)解:若
上的增函数 所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。 (Ⅲ)解:若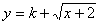 是闭函数,则存在区间[
是闭函数,则存在区间[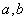 ],
],
在区间[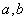 ]上,函数
]上,函数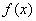 的值域为[
的值域为[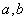 ],即
],即 ,
, 为方程
为方程 的两个实数根即方程
的两个实数根即方程 有两个不等的实根。当
有两个不等的实根。当 时,有
时,有 ,
,
解得 当
当 时,有
时,有 ,无解
,无解
综上所述,

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
已知函数y=sin 在区间[0,t]上至少取得2次最大值,则正整数t的最小值是( )
在区间[0,t]上至少取得2次最大值,则正整数t的最小值是( )

|
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 的图像如左图所示,则函数
的图像如左图所示,则函数 的图像可能是( )
的图像可能是( )
 在区间[0,2π]上的解的个数为 ( ) A.0 B.1 C.2 D.4
在区间[0,2π]上的解的个数为 ( ) A.0 B.1 C.2 D.4 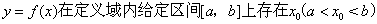 ,满足
,满足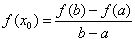 ,则称函数
,则称函数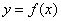 是
是 上的“平均值函数”,
上的“平均值函数”,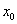 是它的一个均值点.如
是它的一个均值点.如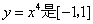 上的平均值函数,0就是它的均
上的平均值函数,0就是它的均 值点.现有函数
值点.现有函数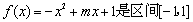 上的平均值函数,则实数
上的平均值函数,则实数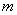 的取值范围是
的取值范围是  ,则
,则 的最大值为_______.
的最大值为_______. 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,则
,则 _______
_______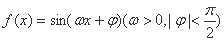 的部分图象如图示,将y=f(x)的图象向右平移
的部分图象如图示,将y=f(x)的图象向右平移 个单位后得到函数y=g(x)的图象.
个单位后得到函数y=g(x)的图象.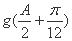 +
+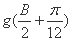 =2
=2 sinAsinB,且C=
sinAsinB,且C=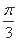 ,c=3,求ΔABC的面积.
,c=3,求ΔABC的面积.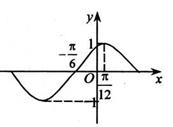
 是偶函数 ②函数
是偶函数 ②函数 的最小正周期是
的最小正周期是 ;
; 在
在 上是增函数;
上是增函数; 的图像的一条对称轴为直线
的图像的一条对称轴为直线 ,则
,则 .
.