题目内容
已知定义在区间(0，＋∞)上的函数f(x)满足f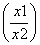
＝f(x1)－f(x2)，且当x＞1时，f(x)＜0.
(1)求f(1)的值；
(2)判断f(x)的单调性；
(3)若f(3)＝－1， f(x)在区间上是否存在最小值，若不存在说明理由，若存在求出最小值
练习册系列答案
相关题目
题目内容
已知定义在区间(0，＋∞)上的函数f(x)满足f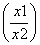＝f(x1)－f(x2)，且当x＞1时，f(x)＜0.
(1)求f(1)的值；
(2)判断f(x)的单调性；
(3)若f(3)＝－1， f(x)在区间上是否存在最小值，若不存在说明理由，若存在求出最小值
、
、
、
、
、
个点）两次，落在水平桌面后，记正面朝上的点数分别为
,
,设事件
为“
为偶数”， 事件
为
”，则概率
等于 。
表示
三个数中的最小值。设
，则
的最大值为
A，求实数m的取值范围．
的两个焦点
，点P是双曲线上一点，
成等比数列，则双曲线的离心率为（ ）
D 
在
处取到极值，则
的值为( )
B.
C.0 D.
n项和为Sn，a1＝1且Sn－1＋
＋2＝0(n≥2)，计算S1，S2，S3，S4，并猜想Sn的表达式．