题目内容
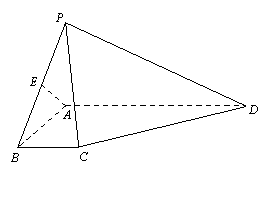
如图,PA⊥平面ABCD,AD//BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.
(1)求证:AE⊥平面PBC;
(2)求二面角B-PC-D的余弦值.
 |
(1)根据题意,建立如图所示的空间直角坐标系,
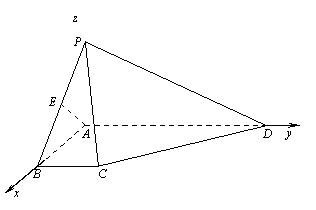 则A(0,0,0),B(1,0,0),C(1,1,0),
则A(0,0,0),B(1,0,0),C(1,1,0),
D(0,3,0),P(0,0,1),E(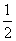 ,0,
,0,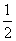 ),
),
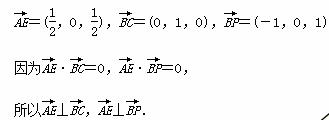 所以AE⊥BC,AE⊥BP.
所以AE⊥BC,AE⊥BP.
因为BC,BP 平面PBC,且BC∩BP=B,
平面PBC,且BC∩BP=B,
所以AE⊥平面PBC.
(2)设平面PCD的法向量为n=(x,y,z),则n· =0,n·
=0,n· =0.
=0.
因为 =(-1,2,0),
=(-1,2,0), =(0,3,-1),所以-x+2y=0,3y-z=0.
=(0,3,-1),所以-x+2y=0,3y-z=0.
令x=2,则y=1,z=3.
所以n=(2,1,3)是平面PCD的一个法向量.
因为AE⊥平面PBC,所以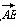 是平面PBC的法向量.
是平面PBC的法向量.
 根据图形可知,二面角B-PC-D的余弦值为-
根据图形可知,二面角B-PC-D的余弦值为-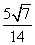 .
.

练习册系列答案
相关题目
 ,已知椭圆
,已知椭圆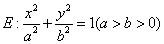 过点
过点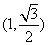 ,且椭圆
,且椭圆 的离心率为
的离心率为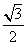 .
. 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆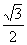 的椭圆T:
的椭圆T: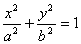 (
(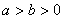 )相切于点M
)相切于点M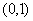 .
.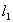 、
、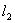 与两曲线分别交于点A、C与点B、D(均不重合).
与两曲线分别交于点A、C与点B、D(均不重合).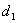 、
、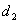 ,求
,求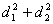 的最大值;
的最大值;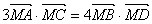 ,求
,求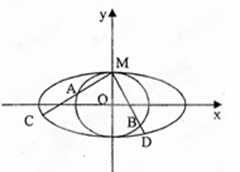
 中,设直线
中,设直线 与圆
与圆 交于
交于 两点,
两点, 为坐标原点,若圆上一点
为坐标原点,若圆上一点 满足
满足 ,则
,则 .
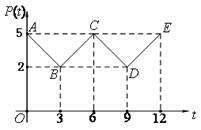
.  (单位:吨)与上市时间
(单位:吨)与上市时间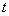 (单位:月)的关系大致如图(1)所示的折线
(单位:月)的关系大致如图(1)所示的折线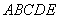 表示,销售价格
表示,销售价格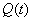 (单位:元/千克)与上市时间
(单位:元/千克)与上市时间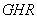 表示(
表示(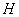 为顶点).
为顶点).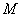 ,动点
,动点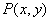 在
在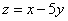 的最大值;
的最大值;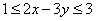 类比为
类比为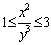 ),试列出
),试列出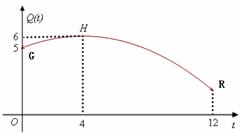
 ,则目标函数z=y-2x的最小值为( )
,则目标函数z=y-2x的最小值为( ) 个面包分给
个面包分给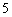 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的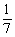 是较小的两份之和,则最小
是较小的两份之和,则最小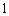 份为( )
份为( )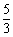 B.
B.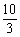 C.
C.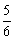 D.
D.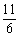
 :
: ,
, :
: ,则
,则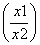 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.