题目内容
6.设?x?表示不小于实数x的最小整数,如?2.6?=3,?-3.5?=-3.已知函数f(x)=?x?2-2?x?,若函数F(x)=f(x)-k(x-2)+2在(-1,4]上有2个零点,则k的取值范围是( )| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $[{-1,-\frac{2}{3}})∪[5,10)$ | C. | $({-\frac{4}{3},-1}]∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
分析 根据[x]的定义,分别作出函数y=f(x)和y=k(x-2)-2的图象,利用数形结合即可得到结论.
解答 解:令F(x)=0得f(x)=k(x-2)-2,
作出函数y=f(x)和y=k(x-2)-2的图象如下图所示:
若函数F(x)=f(x)-k(x-2)+2在(-1,4]上有2个零点,
则函数f(x)和g(x)=k(x-2)-2的图象在(-1,4]上有2个交点,
经计算可得kPA=5,kPB=10,kPO=-1,kPC=-$\frac{2}{3}$,
∴k的范围是[-1,-$\frac{2}{3}$)∪[5,10).
故选:B.
点评 本题考查了对新定义的理解,函数零点的个数与函数图象的关系,数形结合解题思想,属于中档题.

练习册系列答案
相关题目
14.已知偶函数f(x)在区间(-∞,0]内单调递减,a=f(log23),b=f(log45),$c=f({2^{\frac{1}{2}}})$,则a,b,c满足( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
1.在△ABC中,AB=2,BC=$\sqrt{10}$,cosA=$\frac{1}{4}$,则AB边上的高等于( )
| A. | $\frac{3\sqrt{15}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{15}}{2}$ | D. | 3 |
11.直线x=a分别与曲线y=2(x+1),y=x+lnx交于A、B两点,则|AB|的最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3}{2}$ |
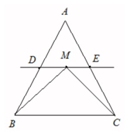 在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.
在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.