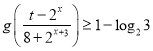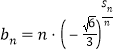题目内容
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在实数
,若存在实数![]() 及
及![]() 、
、![]() (
(![]() )使得对于任意
)使得对于任意![]() 都有
都有![]() 成立,则称函数
成立,则称函数![]() 是带状函数;若
是带状函数;若![]() 存在最小值
存在最小值![]() ,则称
,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,请说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,请说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() 是带状函数的充要条件是
是带状函数的充要条件是![]() .
.
【答案】(1)是,带宽为2;(2)证明见解析;(3)证明见解析
【解析】
(1)根据函数关系![]() ,即可判定是带状函数;
,即可判定是带状函数;
(2)分别证明![]() 即可得证;
即可得证;
(3)处理绝对值,将函数写成分段函数形式,分别证明充分性和必要性.
(1)考虑两条直线,即: ![]() ,
,
断函数![]() 是带状函数,带宽为2;
是带状函数,带宽为2;
(2)函数![]() (
(![]() ),
),
当![]() 时,
时,![]() 所以有
所以有![]() ,有
,有![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
所以有![]() ,
,![]() 所以
所以![]() ,
,
综上所述![]() ,
,
所以函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)函数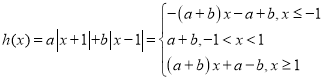 ,
,
充分性:当![]() 时,
时,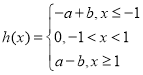 ,
,
![]() ,存在两条直线
,存在两条直线![]() 满足题意,即该函数
满足题意,即该函数![]() 为带状函数;
为带状函数;
必要性:当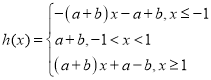 为带状函数,
为带状函数,
则存在![]() ,
,
假设![]()
不妨考虑![]() ,
,
则直线![]() 与两条直线
与两条直线![]() 中至少一条相交,所以不满足
中至少一条相交,所以不满足![]() ,
,
所以![]() 不满足题意.即
不满足题意.即![]() ,
,
综上所述:函数![]() 是带状函数的充要条件是
是带状函数的充要条件是![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目