题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上奇函数
上奇函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式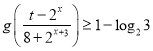 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)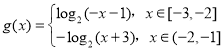 (3)
(3)![]()
【解析】
(1)根据对数函数单调性以及定义域化简解不等式,再解分式不等式得结果;
(2)先根据奇函数性质求得![]() ,再根据奇函数以及条件将要求自变量转化到已知区间,最后根据已知区间解析式求结果;
,再根据奇函数以及条件将要求自变量转化到已知区间,最后根据已知区间解析式求结果;
(3)先根据函数性质解得一个周期下的不等式解集,再根据![]() 范围确定包含关系,解得结果.
范围确定包含关系,解得结果.
解:(1)原不等式可化为![]() ,
,
∴![]() ,且
,且![]() ,且
,且![]() ,
,
得![]() .
.
(2)∵![]() 是奇函数,∴
是奇函数,∴![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
当![]() 时,
时, ![]() ,
, ![]() .
.
∴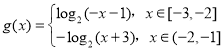
(3)∵![]()
![]() ,即
,即![]() 周期为4,
周期为4,
因为![]() 为奇函数,且当
为奇函数,且当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]()
因为![]() ,
,
所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]()
在一个周期![]() 内,
内,![]()
记![]() ,
,
当![]() 时,
时,![]() ,
,
因为关于![]() 的不等式
的不等式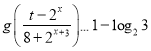 在
在![]() 上恒成立,
上恒成立,
∴![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,
,
因为关于![]() 的不等式
的不等式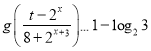 在
在![]() 上恒成立,
上恒成立,
所以![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
