题目内容
如图,在四棱锥 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,
,  底面
底面 ,
, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.

(Ⅰ)求四棱锥 的体积;
的体积;
(Ⅱ)证明:直线 平面
平面 .
.
 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,
,  底面
底面 ,
, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求四棱锥
 的体积;
的体积;(Ⅱ)证明:直线
 平面
平面 .
.(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)求四棱锥
 的体积,由体积公式
的体积,由体积公式 ,由已知
,由已知 底面
底面 ,显然
,显然 是高,且值为2,而底面是边长为
是高,且值为2,而底面是边长为 的菱形,
的菱形, ,,有平面几何知识,可求得面积
,,有平面几何知识,可求得面积 ,代入公式,可求得体积;(Ⅱ)证明:直线
,代入公式,可求得体积;(Ⅱ)证明:直线 平面
平面 ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题虽有中点,但没直接的三角形,可考虑用平行四边形的对边平行,可取OD的中点G,连结CG,MG,证明四边形
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题虽有中点,但没直接的三角形,可考虑用平行四边形的对边平行,可取OD的中点G,连结CG,MG,证明四边形 为平行四边形即可,也可取
为平行四边形即可,也可取 中点
中点 ,连接
,连接 ,
, ,利用面面平行则线面平行,证平面
,利用面面平行则线面平行,证平面 平面
平面 即可.
即可.试题解析:(Ⅰ)

(Ⅱ)取
 中点
中点 ,连接
,连接 ,
, ,
, ,又
,又
 ,
, .
.
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
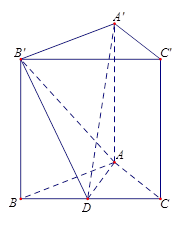
 B'D;
B'D;
 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 分别是
分别是 的中点
的中点
 ∥平面
∥平面 ;
; ;
; 的体积.
的体积.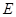 是以
是以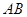 为直径的半圆上异于点
为直径的半圆上异于点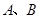 的点,矩形
的点,矩形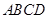 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且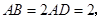
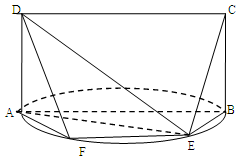
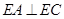 ;
;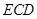 与半圆弧的另一个交点为
与半圆弧的另一个交点为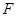 ,
,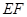 //
//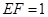 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积.



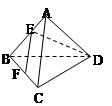
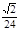 B.
B. 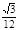 C.
C.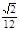 D.
D.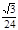
 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 ,则此棱锥的体积为 .
,则此棱锥的体积为 .