题目内容
20.若函数$f(x)=\left\{{\begin{array}{l}\begin{array}{l}{x^2}+2x-5,x>0\\ a,x=0\end{array}\\{g(x),\;\;x<0\;\;\;\;\;\;\;\;}\end{array}}\right.$为奇函数,则a=0,f(g(-1))=3.分析 直接利用奇函数的定义,即可得出结论.
解答 解:由题意,a=f(0)=0,
g(-1)=-g(1)=2,
∴f(g(-1))=f(2)=3,
故答案为:0,3.
点评 本题考查函数值的计算,考查奇函数的定义,比较基础.

练习册系列答案
相关题目
10.已知三棱柱ABC-A1B1C1的底面是锐角三角形,则存在过点A的平面( )
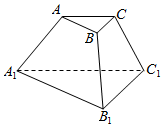

| A. | 与直线BC和直线A1B1都平行 | B. | 与直线BC和直线A1B1都垂直 | ||
| C. | 与直线BC平行且直线A1B1垂直 | D. | 与直线BC和直线A1B1所成角相等 |
11.若不等式x2+mx-m>0,的解集为R,则实数m的取值范围是( )
| A. | m<-4或m>0 | B. | m<0或m>4 | C. | -4<m<0 | D. | 0<m<4 |
8.已知点A(4,0),抛物线C:x2=12y的焦点为F,射线FA与抛物线和它的准线分别相交于点M和N,则|FM|:|MN|等于( )
| A. | 2:3 | B. | 3:4 | C. | 3:5 | D. | 4:5 |
15.已知集合M={0,1,2,3,4},N={x|1<log2(x+2)<2},则M∩N=( )
| A. | {0,1} | B. | {2,3} | C. | {1} | D. | {2,3,4} |
9.同时掷2枚硬币,那么互为对立事件的是( )
| A. | 恰好有1枚正面和恰有2枚正面 | B. | 至少有1每正面和恰好有1枚正面 | ||
| C. | 至少有2枚正面和恰有1枚正面 | D. | 最多有1枚正面和恰有2枚正面 |
10.已知x,y∈[0,2],对于任意的m,n∈{1,2,3},不等式$\sqrt{{x}^{2}+{y}^{2}}$>|m-n|恒成立的概率为( )
| A. | $\frac{1}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{16}$ |