题目内容
12.已知某三棱锥的三视图如图所示,则该三棱锥的体积为8,最长棱的棱长为2$\sqrt{10}$.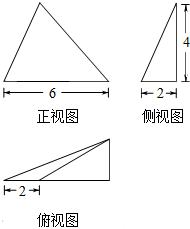
分析 根据几何体的三视图,得出该几何体是侧面垂直于底面的三棱锥,画出图形,结合图形求出它的体积与最长的棱长即可.
解答 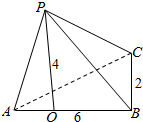 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是侧面PAB⊥底面ABC的三棱锥,如图所示;
过点P作PO⊥AB,垂足为O,
则PO=4,
三棱锥P-ABC的体积为$\frac{1}{3}$×$\frac{1}{2}$×6×2×4=8;
三棱锥P-ABC的各条棱长为AB=6,BC=2,AC=$\sqrt{{6}^{2}{+2}^{2}}$=2$\sqrt{10}$,
PA=$\sqrt{{4}^{2}{+2}^{2}}$=2$\sqrt{5}$,PB=$\sqrt{{4}^{2}{+4}^{2}}$=4$\sqrt{2}$,PC=$\sqrt{{2}^{2}{+(4\sqrt{2})}^{2}}$=6;
所以最长的棱是AC=2$\sqrt{10}$.
故答案为:8,$2\sqrt{10}$
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期是π,若其图象向右平移$\frac{π}{6}$个单位,得到的函数为偶函数,则函数f(x)的图象( )
| A. | 关于直线x=$\frac{5π}{12}$对称 | B. | 关于点($\frac{7π}{12}$,0)对称 | ||
| C. | 关于点($\frac{5π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
4.将样本数据按某标准分组,并制成频率分布直方图,已知样本数据在其中一组[m,n)中的频率为p,且该组在频率分布直方图上的高为h,则|m-n|等于( )
| A. | $\frac{p}{h}$ | B. | $\frac{h}{p}$ | C. | ph | D. | 与h,p无关 |
2.已知A、B、C三点不共线,且$\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$+2$\overrightarrow{AC}$,则$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | 6 | D. | $\frac{1}{6}$ |