题目内容
已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作平面α∥AB.
(1)求证:CD∥α;
(2)若AB=4,EF=![]() ,CD=2,求AB与CD所成角的大小.
,CD=2,求AB与CD所成角的大小.
(1)证明:如图4,连接AD交α于G,连接GF,
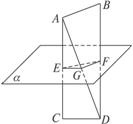
图4
∵AB∥α,面ADB∩α=GF![]() AB∥GF.
AB∥GF.
又∵F为BD中点,
∴G为AD中点.
又∵AC、AD相交,确定的平面ACD∩α=EG,E为AC中点,G为AD中点,∴EG∥CD.
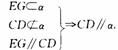
(2)解:由(1)证明可知:
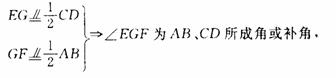
∵AB=4,GF=2,CD=2,∴EG=1,EF=![]() .
.
在△EGF中,由勾股定理,得∠EGF=90°,即AB与CD所成角的大小为90°.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 已知AB与CD为异面线段,CD?平面α,AB∥α,M、N分别是线段AC与BD的中点,求证:MN∥平面α.
已知AB与CD为异面线段,CD?平面α,AB∥α,M、N分别是线段AC与BD的中点,求证:MN∥平面α.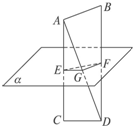 已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作 平面α∥AB.
已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作 平面α∥AB.