题目内容
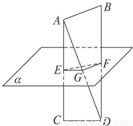
已知AB与CD为异面线段，CD?平面α，AB∥α，M、N分别是线段AC与BD的中点，求证：MN∥平面α．分析：连结AD，并取AD中点E，利用三角形中位线性质可得NE∥AB，可得NE∥α．再证明ME∥α，可得平面MEN∥平面α，从而证得MN∥平面α．
解答：
证明：如图：根据已知AB与CD为异面线段，可得A、B、C、D不共面．
连结AD，并取AD中点E，可得M、N、E不共线，故M、N、E确定一个平面．
∵N是BD的中点，∴NE∥AB．
又AB∥α，∴NE∥α．
∵M是AC的中点，∴ME∥CD，再由CD?平面α，ME不在平面α内，可得ME∥α，
∵ME∩NE=E，∴平面MEN∥平面α，∴MN∥平面α．
证明：如图：根据已知AB与CD为异面线段，可得A、B、C、D不共面．连结AD，并取AD中点E，可得M、N、E不共线，故M、N、E确定一个平面．
∵N是BD的中点，∴NE∥AB．
又AB∥α，∴NE∥α．
∵M是AC的中点，∴ME∥CD，再由CD?平面α，ME不在平面α内，可得ME∥α，
∵ME∩NE=E，∴平面MEN∥平面α，∴MN∥平面α．
点评：本题主要考查直线和平面平行的判定定理的应用，两个平面平行的性质，属于中档题．
练习册系列答案
相关题目
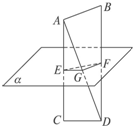已知AB、CD为异面线段，E、F分别为AC、BD中点，过E、F作 平面α∥AB．
,CD=2,求AB与CD所成的角的大小.
，CD=2，求AB与CD所成角的大小.
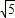，CD=2，求AB与CD所成角的大小．