题目内容
已知AB、CD为异面直线,E、F分别为AC、BD的中点,过E、F作平面α∥AB.(1)求证:CD∥α;
(2)若AB=4,EF=7,CD=2,求AB、CD所成角的大小.
(1)证明:如图所示,连结BC,交平面α于点O,

∵AB∥α,平面ABC∩α=EO,
∴AB∥EO.
又∵E为AC中点,
∴O为BC中点.
又BF=FD,
∴OF∥CD.
∴CD∥α.
(2)解:由题意可知,E、O、F三点不共线,否则AB∥CD.
在△EOF中,EF=![]() ,OE=
,OE=![]() AB=2,OF=
AB=2,OF=![]() CD=1.由余弦定理,cos∠EOF
CD=1.由余弦定理,cos∠EOF
=![]() =-
=-![]() .
.
因此异面直线AB、CD所成的角是60°.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 已知AB与CD为异面线段,CD?平面α,AB∥α,M、N分别是线段AC与BD的中点,求证:MN∥平面α.
已知AB与CD为异面线段,CD?平面α,AB∥α,M、N分别是线段AC与BD的中点,求证:MN∥平面α.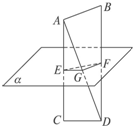 已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作 平面α∥AB.
已知AB、CD为异面线段,E、F分别为AC、BD中点,过E、F作 平面α∥AB.