题目内容

下列函数中，周期为1且为奇函数的是（　　）
A、y=1-sin2πx
B、y=tanπx
C、y=cos（πx+
π
2
）
D、y=cos2πx-sin2πx
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：利用三角函数的周期性与奇偶性判断即可．
解答： 解：观察A、B、C、D四个选项，可知B：y=tanπx与C：y=cos（πx+
π
2
）为奇函数，另外两个不是，可排除A与D，
又y=tanπx的周期T=
π
π
=1，符合题意，而y=cos（πx+
π
2
）的周期T=
2π
π
=2≠1，可排除C，
故选：B．
点评：本题考查三角函数的周期性及其求法，考查三角函数的奇偶性，属于基本知识的考查．
练习册系列答案
相关题目
数列{an}的前n项和记为Sn，a1=1，an+1=2Sn+1（n≥1，n∈N），则数列{an}的通项公式是（　　）
A、an=2n
B、an=2n-1
C、an=3n-1
D、an=3n
直线y=x与椭圆
x2
4
+y2=1相交于A，B两点，则|AB|=（　　）
A、2
B、
4
5
5
C、
4
10
5
D、
8
10
5
函数f（x）=sin（-2x+
π
3
）的最小正周期是
 
．
已知某单位有50名职工，从中按系统抽样抽取10名职工．
（1）若第5组抽出的号码为22，写出所有被抽出职工的号码；
（2）分别统计这10名职工的体重（单位：公斤），获得体重数据的茎叶图如图所示，现从这10名职工中随机抽取两名体重超过平均体重的职工，求体重为76公斤的
职工被抽取到的概率．
已知向量
m
=（ex，lnx+k），
n
=（1，f（x）），
m
∥
n
（k为常数，e是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与y轴垂直，F（x）=xexf′（x）．
（1）求k的值；
（2）求F（x）的单调区间及最大值．
已知命题P：函数f（x）=x3+mx2+mx-m既有极大值又有极小值；命题Q：?x∈R，x2+mx+1≥0，如果“P∨Q”为真命题，“P∧Q”为假命题，求实数m的取值范围．
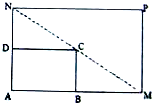如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B点在AM上，D点在AN上，且对角线MN过C点，已知AB=3米，AD=2米．
（Ⅰ）要使花坛AMPN的面积大于32平方米，求AN长的取值范围；
（Ⅱ）若AN∈[3，4）（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积．
已知向量
AB
=（2，x-1），
CD
=（1，-y），其中xy＞0，且
AB
∥
CD
，则
8x+y
xy
的最小值为（　　）
A、34B、25C、27D、16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网