题目内容
已知点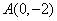 ,椭圆
,椭圆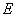 :
: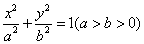 的离心率为
的离心率为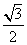 ,
,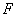 是椭圆的焦点,直线
是椭圆的焦点,直线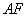 的斜率为
的斜率为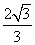 ,
, 为坐标原点.
为坐标原点.
(1)求椭圆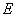 的方程;
的方程;
(2)设过点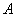 的直线
的直线 与椭圆
与椭圆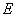 相较于
相较于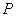 ,
,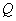 两点,当△
两点,当△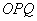 的面积最大时,求
的面积最大时,求 的方程.
的方程.
解: (1)显然 是椭圆的右焦点,设
是椭圆的右焦点,设
由题意
 ………2分
………2分
又离心率
 ,
,
故椭圆 的方程为
的方程为 …………4分
…………4分
(2)由题意知,直线 的斜率存在,设直线
的斜率存在,设直线 的斜率为
的斜率为 ,方程为
,方程为
联立直线与椭圆方程: ,化简得:
,化简得: .
.
∵ ,∴
,∴ ,
,
设 ,则
,则  ……………7分
……………7分
∴ .
.
坐标原点 到直线
到直线 的距离为
的距离为 ……………9分
……………9分

令  ,则
,则  ……………12分
……………12分
 (当且仅当
(当且仅当  即
即 时等号成立)
时等号成立)
故当 即
即  ,
, 时
时 的面积最大
的面积最大
从而直线 的方程为
的方程为 

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
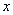 为实数,
为实数, 表示不超过
表示不超过 在
在 上为
上为  ,可以采用以下方法:
,可以采用以下方法: ,
,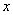 求导,得
求导,得 ,
, ,得
,得 ,
, .
. 的左焦点与抛物线
的左焦点与抛物线 的焦点重合,斜率为1的直线
的焦点重合,斜率为1的直线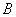 两点,若
两点,若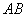 中点坐标为
中点坐标为 ,则双曲线的离心率为
,则双曲线的离心率为 B.
B. C.
C. D.
D.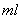 和700
和700 的值;
的值;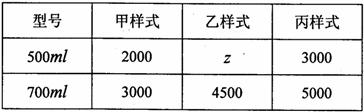
 ,则输出的
,则输出的 ( )
( ) B.
B. C.
C. D.
D.

 ,若对于任意的
,若对于任意的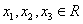
 ,
,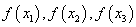 为某一三角形的三边长,则称
为某一三角形的三边长,则称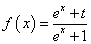 是“可构成三角形的函数”,则实数
是“可构成三角形的函数”,则实数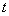 的取值范围是( )
的取值范围是( )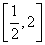 B.
B. 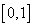 C.
C.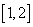 D.
D.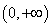
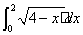 ,那么a2014(a2012+2a2014+a2016)的值为 ( )
,那么a2014(a2012+2a2014+a2016)的值为 ( )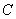 的极坐标方程为
的极坐标方程为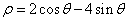 .以极点为原点,极轴为
.以极点为原点,极轴为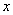 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为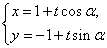 (
(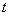 为参数).
为参数).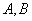 两点,且
两点,且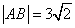 ,求直线
,求直线