题目内容
已知曲线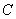 的极坐标方程为
的极坐标方程为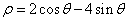 .以极点为原点,极轴为
.以极点为原点,极轴为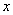 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为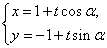 (
(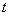 为参数).
为参数).
(Ⅰ)判断直线 与曲线
与曲线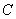 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)若直线 和曲线
和曲线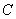 相交于
相交于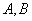 两点,且
两点,且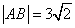 ,求直线
,求直线 的斜率.
的斜率.
解:(Ⅰ)  ,
, , 1分
, 1分
 曲线
曲线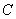 的直角坐标方程为
的直角坐标方程为 ,即
,即 , 3分
, 3分
 直线
直线 过点
过点 ,且该点到圆心的距离为
,且该点到圆心的距离为 ,
, 直线
直线 与曲线
与曲线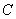 相交. 4分
相交. 4分
(Ⅱ)解法一:当直线 的斜率不存在时,直线
的斜率不存在时,直线 过圆心,
过圆心, , 5分
, 5分
则直线 必有斜率,设其方程为
必有斜率,设其方程为 ,即
,即 ,
,
圆心到直线 的距离
的距离 , 6分
, 6分
解得 ,
, 直线
直线 的斜率为
的斜率为 . 7分
. 7分
解法二:将 代入
代入 ,得
,得 ,
,
整理得, , 5分
, 5分
设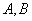 两点对应的参数分别为
两点对应的参数分别为 ,则
,则 ,
,
 , 6分
, 6分
不妨设 为直线的
为直线的 的倾斜角,则
的倾斜角,则 ,则
,则 或
或 ,
, 直线
直线 的斜率为
的斜率为 . 7分
. 7分

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
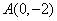 ,椭圆
,椭圆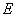 :
: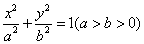 的离心率为
的离心率为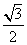 ,
,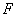 是椭圆的焦点,直线
是椭圆的焦点,直线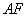 的斜率为
的斜率为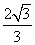 ,
, 为坐标原点.
为坐标原点.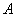 的直线
的直线 与椭圆
与椭圆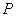 ,
,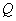 两点,当△
两点,当△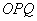 的面积最大时,求
的面积最大时,求 ,AB=AC=2
,AB=AC=2 ,BAC=90,G为△PAB的重心.
,BAC=90,G为△PAB的重心.
 及
及 .类比之,
.类比之,
 ,
, 恒成立,
恒成立,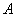 等于
等于
 B.
B.
 D.
D.
 ,求证:CP∥平面ABEF;
,求证:CP∥平面ABEF;
 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为
的值为  ”是真命题,则实数a的取值范围是
”是真命题,则实数a的取值范围是  为偶函数,
为偶函数, ,其图象与直线
,其图象与直线 的某两个交点的横坐标为
的某两个交点的横坐标为 ,若|
,若| |的最小值为
|的最小值为 ,则( )
,则( ) B.
B.  C.
C.  D.
D. 