题目内容
14．已知函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}a{x}^{2}$+bx在[1，2]上为减函数，求a+b的最小值．分析 求导函数，利用y=f（x）在区间[1，2]上是单调减函数，建立不等式，将a+b用条件线性表示，即可求得a+b的最小值．
解答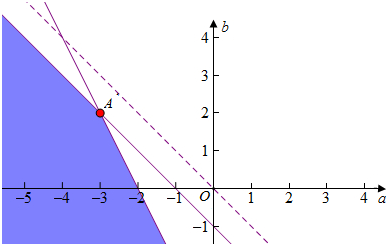 
解：f′（x）=x2+ax+b，
因为函数f（x）在区间[1，2]上是减函数即在区间[1，2]上，f′（x）≤0，
∴$\left\{\begin{array}{l}{f′（1）≤0}\\{f′（2）≤0}\end{array}\right.$，即$\left\{\begin{array}{l}{1+a+b≤0}\\{4+2a+b≤0}\end{array}\right.$
即$\left\{\begin{array}{l}{a+b≤-1}\\{2a+b≤-4}\end{array}\right.$
在坐标平面内作直线 a+b+1=0、2a+b+4=0，它们交于 A（-3，2），
满足①（a，b）是 A 点上方区域，
令a+b=t，则 b=-a+t，t是直线在b轴上的截距，
平移直线，可以看出，当直线过A时，
t最小为-3+2=-1．
故a+b的最小值是-1．
点评 本题主要考查了导数与函数的单调性的问题，以及区域线性规划，属于中档题．
练习册系列答案
相关题目
2．设f（x）为定义在R上的奇函数，当x≥0时，有f（x）=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}（x+1），\;x∈[0，1）\\ 1-|x-3|，\;x∈[1，+∞）.\end{array}$，则关于x的函数F（x）=f（x）-$\frac{1}{2}$的所有零点之和为（ ）
| A． | $\sqrt{2}$-1 | B． | $\frac{{\sqrt{2}}}{2}$-1 | C． | 1-$\frac{{\sqrt{2}}}{2}$ | D． | 1-$\sqrt{2}$ |
19．点P是曲线y=x2-1nx上任意一点，则点P到直线y=x-2的距离的最小值是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
6．将函数f（x）=$sin（2x-\frac{π}{4}）$向右平移$\frac{3π}{8}$个单位，再将所得的函数图象上的各点纵坐标不变，横坐标变为原来的2倍，得到函数y=g（x）的图象，则函数y=g（x）与x=-$\frac{π}{2}$，x=$\frac{π}{3}$，x轴围成的图形面积为（ ）
| A． | $\frac{5}{2}$ | B． | $1+\frac{{\sqrt{3}}}{2}$ | C． | $\frac{3}{2}$ | D． | $1-\frac{{\sqrt{3}}}{2}$ |