题目内容
2.设f(x)为定义在R上的奇函数,当x≥0时,有f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),\;x∈[0,1)\\ 1-|x-3|,\;x∈[1,+∞).\end{array}$,则关于x的函数F(x)=f(x)-$\frac{1}{2}$的所有零点之和为( )| A. | $\sqrt{2}$-1 | B. | $\frac{{\sqrt{2}}}{2}$-1 | C. | 1-$\frac{{\sqrt{2}}}{2}$ | D. | 1-$\sqrt{2}$ |
分析 根据分段函数的解析式和奇函数的对称性作出函数f(x)在R上的图象和y=$\frac{1}{2}$的图象,利用数形结合的方法求解即可.
解答 解:由题意作出函数f(x)在R上的图象和y=$\frac{1}{2}$的图象如下,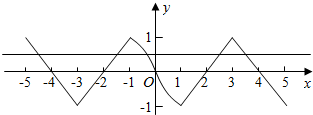 ,
,
由图象可知函数$F(x)=f(x)-\frac{1}{2}$共有5个零点,
其中最左边两个零点x1+x2=-6,
最右边两个零点x4+x5=6,
中间一个零点x3是方程${log_2}(1-x)=\frac{1}{2}$的根,
解得${x_3}=1-\sqrt{2}$,
故所有零点之和为x1+x2+x3+x4+x5=$1-\sqrt{2}$;
故选D.
点评 本题考查了分段函数的应用及数形结合的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知(x2+$\frac{1}{x}$)6的展开式中的常数项为a,则直线y=ax与曲线y=x3围成的封闭图形的面积为( )
| A. | 450 | B. | 225 | C. | $\frac{225}{2}$ | D. | $\frac{225}{4}$ |
10.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A,若该双曲线右支上存在两点B,C使得△ABC为等腰直角三角形,则该双曲线的离心率e的取值范围是( )
| A. | (1,3) | B. | ($1,\sqrt{3}$) | C. | (1,2) | D. | ($1,\sqrt{2}$) |
7.设f(x)=xsinx,x∈$[{-\frac{π}{2},\frac{π}{2}}]$,若f(x1)>f(x2),则下列不等式中必定成立的是( )
| A. | x1-x2<0 | B. | x1-x2>0 | C. | x12-x22>0 | D. | x12<x22 |
11.设函数f(x)=loga|x+b|在定义域内具有奇偶性,f(b-2)与f(a+1)的大小关系是( )
| A. | f(b-2)=f(a+1) | B. | f(b-2)>f(a+1) | C. | f(b-2)<f(a+1) | D. | 不能确定 |