题目内容
15.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F且垂直于x轴的直线在第一象限内与C、C的渐近线的交点分别为A、B,若A是BF的中点,则C的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
分析 根据条件求出A,B的坐标,结合中点坐标公式建立a,c的关系进行求解即可.
解答 解:根据题意可求得A(c,$\frac{{b}^{2}}{a}$),B(c,$\frac{bc}{a}$),
∵A为BF的中点,∴2•$\frac{{b}^{2}}{a}$=$\frac{bc}{a}$,即c=2b,
∴双曲线C的离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{c}^{2}}{{c}^{2}-{b}^{2}}}$=$\frac{2\sqrt{3}}{3}$.
故选:A
点评 本题主要考查双曲线离心率的计算,根据直线和双曲线的相交关系求出交点坐标,结合中点坐标公式以及离心率的公式是解决本题的关键.

练习册系列答案
相关题目
3.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)焦点与实轴垂直的直线与双曲线的两条渐近线交于A,B两点,与双曲线交于M,N两点,若M,N为线段AB的两个三等分点,则双曲线的离心率为( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
10.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的离心率$\sqrt{5}$,则该双曲线的一条渐近线被圆C:x2+y2-2x-3=0截得的弦长为( )
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{8\sqrt{5}}}{5}$ | C. | 3 | D. | 2 |
7.以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆与双曲线的离心率之积为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
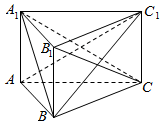 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°.