题目内容
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程;
(3)若动圆P过点N(-2,0),且与矩形ABCD的外接圆外切,求动圆P的圆心的轨迹方程.
解:(1)因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,所以直线AD的斜率为-3.又因为点T(-1,1)在直线AD上,所以AD边所在直线方程为y-1=-3(x+1),即3x+y+2=0.
(2)由![]() 解得A的坐标为(0,-2),因为矩形ABCD两条对角线交点为M(2,0),所以M为矩形ABCD外接圆圆心,又|AM|=
解得A的坐标为(0,-2),因为矩形ABCD两条对角线交点为M(2,0),所以M为矩形ABCD外接圆圆心,又|AM|=![]() ,从而矩形ABCD外接圆的方程为(x-2)2+y2=8.
,从而矩形ABCD外接圆的方程为(x-2)2+y2=8.
(3)因为动圆P过点N,所以|PN|是该圆半径,又∵动圆P与圆M外切,∴|PM|=|PN|+2![]() ,即|PM|-|PN|=2
,即|PM|-|PN|=2![]() .
.
故点P的轨迹是以M,N为焦点,实轴长为22的双曲线左支.
∵a=![]() ,c=2,∴b2=2.故所求轨迹方程为
,c=2,∴b2=2.故所求轨迹方程为
![]() =1(x≤-
=1(x≤-![]() ).
).

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
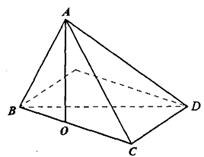 如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
△ABD折起,使A点在平面BCD内的射影落在
BC边上,若二面角C—AB—D的平面有大小为
θ,则sinθ
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
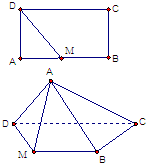 如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起, BC=2 点E为BC的中点,点F在CD上。若
BC=2 点E为BC的中点,点F在CD上。若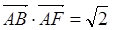 则
则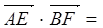 _____________。
_____________。
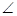 BCF=
BCF= ,AD=
,AD=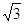 ,EF=2.
,EF=2.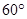 .
.