题目内容
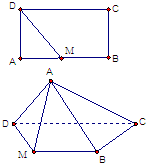 如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,(1)在DC上是否存在一点N,不论△AMD折到什么位置(不与平面MBCD重合),总有MD∥平面ABN?
(2)当二面角A-MD-C的大小为60°时,求四棱锥A-MBCD的体积.
分析:(1)取N为DC中点时,连接AN,BN,由三角形中位线定理,我们可证得MBND为平行四边形,进而MD∥BN,由线面平行的判定定理可得MD∥平面ABN;
(2)取MD的中点E,连接AE,NE,取EN中点F,连接AF,由已知结合二面角平面角的定义,可得∠AEN是二面角A-MD-C的平面角,即∠AEN=60°,进而由AF⊥EN,DM⊥AF,得到AF为平面MBCD上的高,求出底面MBCD的面积后,代入棱锥体积公式,即可得到四棱锥A-MBCD的体积.
(2)取MD的中点E,连接AE,NE,取EN中点F,连接AF,由已知结合二面角平面角的定义,可得∠AEN是二面角A-MD-C的平面角,即∠AEN=60°,进而由AF⊥EN,DM⊥AF,得到AF为平面MBCD上的高,求出底面MBCD的面积后,代入棱锥体积公式,即可得到四棱锥A-MBCD的体积.
解答:解:(1)当N为DC中点时,连接AN,BN,
∵MB∥DC,且MB=
DC=DN,∴MBND为平行四边形∴MD∥BN,…(2分)
又MD?平面ABN,且BN?平面ABN,因此MD∥平面ABN…(4分)
(2)取MD的中点E,连接AE,NE,取EN中点F,连接AF
∵在矩形ABCD中,AD=AM=1,∴AMND是正方形,
∴AE⊥DM,NE⊥DM,故∠AEN是二面角A-MD-C的平面角…(6分)
即∠AEN=60°,又AE=NE,∴△AEN是正三角形,所以AF⊥EN,又因为DM⊥AF,
∴AF⊥平面MBCD,易得SMBCD=
,AF=
…(10分)
∴VA-MBCD=
SMBCD•AF=
•
•
=
…(12分)
∵MB∥DC,且MB=
| 1 |
| 2 |
又MD?平面ABN,且BN?平面ABN,因此MD∥平面ABN…(4分)
(2)取MD的中点E,连接AE,NE,取EN中点F,连接AF
∵在矩形ABCD中,AD=AM=1,∴AMND是正方形,
∴AE⊥DM,NE⊥DM,故∠AEN是二面角A-MD-C的平面角…(6分)
即∠AEN=60°,又AE=NE,∴△AEN是正三角形,所以AF⊥EN,又因为DM⊥AF,
∴AF⊥平面MBCD,易得SMBCD=
| 3 |
| 2 |
| ||
| 4 |
∴VA-MBCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| ||
| 4 |
| ||
| 8 |
点评:本题考查的知识点是二面角的平面角及其求法,直线与平面平行的判定,其中(1)的关键是证得MD∥BN,(2)的关键是构造∠AEN是二面角A-MD-C的平面角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
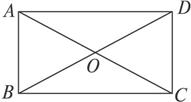
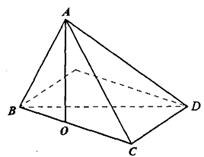 如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
△ABD折起,使A点在平面BCD内的射影落在
BC边上,若二面角C—AB—D的平面有大小为
θ,则sinθ
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
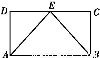
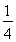
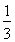
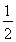

 BC=2 点E为BC的中点,点F在CD上。若
BC=2 点E为BC的中点,点F在CD上。若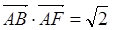 则
则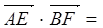 _____________。
_____________。