题目内容
3.命题p:?x∈R,2x+2-x≥2,q:?x0∈R,x02-x0+1=0,则( )| A. | p∨q为真命题 | B. | p∧q为真命题 | C. | ¬p为真命题 | D. | (¬p)∧(¬q)为真命题 |
分析 分别判断出p,q的真假,从而判断出复合命题的真假.
解答 解:命题p:?x∈R,2x+2-x≥2,是真命题,
?x∈R,x2-x+1>0,故q:?x0∈R,x02-x0+1=0,是假命题,
故p∨q是真命题,p∧q是假命题,¬p是假命题,
故选:A.
点评 本题考查了复合命题的真假,考查函数问题,是一道基础题.

练习册系列答案
相关题目
13.经过点A(2,3)和点B(4,7)的直线方程是( )
| A. | 2x+y-7=0 | B. | 2x-y+1=0 | C. | 2x-y-1=0 | D. | -2y+4=0 |
14.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,2),k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$平行,则k的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
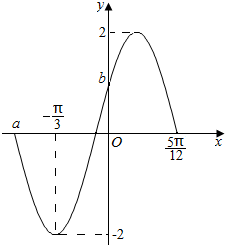 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.