题目内容
12.已知函数f(x)=x2-ax+b(a>0,b>0)有两个不同的零点m,n,且m,n和-2三个数适当排序后,即可成为等差数列,也可成为等比数列,则a+b的值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 由一元二次方程根与系数的关系得到m+n=a,mn=b,再由m,n,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列列关于m,n的方程组,求得m,n后得答案.
解答 解:由题意可得:m+n=a,mn=b,
∵a>0,b>0,
可得m>0,n>0,
又m,n,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,
可得$\left\{\begin{array}{l}{2n=m-2}\\{mn=4}\end{array}\right.$①或$\left\{\begin{array}{l}{2m=n-2}\\{mn=4}\end{array}\right.$②.
解①得:m=4,n=1;解②得:m=1,n=4.
∴a=5,b=4,
则a+b=9.
故选:C.
点评 本题考查了一元二次方程根与系数的关系,考查了等差数列和等比数列的性质,是基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
2.已知a>0且a≠1,下列函数中,在区间(0,a)上一定是减函数的是( )
| A. | f(x)=$\frac{2x-a}{x}$ | B. | f(x)=ax | C. | f(x)=loga(ax) | D. | f(x)=x2-3ax+1 |
3.命题p:?x∈R,2x+2-x≥2,q:?x0∈R,x02-x0+1=0,则( )
| A. | p∨q为真命题 | B. | p∧q为真命题 | C. | ¬p为真命题 | D. | (¬p)∧(¬q)为真命题 |
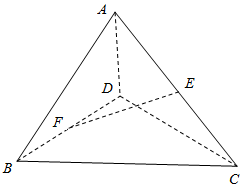 空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.
空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小. 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.