题目内容
18.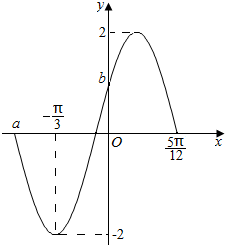 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)求图中a,b的值及函数f(x)的递减区间.
分析 (1)根据三角函数的图象确定A,ω和φ的值即可.
(2)根据三角函数的图象进行求解即可.
解答 解:由图象知A=2,$\frac{3T}{4}$=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{9π}{12}$,则T=π,
即$\frac{2π}{ω}$=π,则ω=2,
即f(x)=2sin(2x+φ),
∵f(-$\frac{π}{3}$)=2sin[2×(-$\frac{π}{3}$)+φ]=-2,
即sin(-$\frac{2π}{3}$+φ)=-1,
∵|φ|<$\frac{π}{2}$,∴-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴-$\frac{7π}{6}$<φ-$\frac{2π}{3}$<-$\frac{π}{6}$,
则φ-$\frac{2π}{3}$=-$\frac{π}{2}$,
即φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$).
(2)∵函数的周期T=$\frac{5π}{12}$-a=π,
∴a=-$\frac{7π}{12}$,
b=f(0)=2sin$\frac{π}{6}$=2×$\frac{1}{2}$=1..
由$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ(k∈Z)得:$\frac{π}{6}$+kπ≤x≤$\frac{2π}{3}$+kπ(k∈Z),
即函数的单调递减区间为[$\frac{π}{6}$+kπ,$\frac{2π}{3}$+kπ],(k∈Z)
点评 本题主要考查三角函数的图象和性质,根据条件求出A,ω和φ的值求出函数的解析式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知集合P={1,3,5,7},Q={x|2x-1>5},则P∩Q等于( )
| A. | {7} | B. | {5,7} | C. | {3,5,7} | D. | {x|3<x≤7} |
3.命题p:?x∈R,2x+2-x≥2,q:?x0∈R,x02-x0+1=0,则( )
| A. | p∨q为真命题 | B. | p∧q为真命题 | C. | ¬p为真命题 | D. | (¬p)∧(¬q)为真命题 |
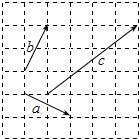 如图,在6×6的方格中,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$的起点和终点均在格点,且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),那么x+y=3.
如图,在6×6的方格中,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$的起点和终点均在格点,且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),那么x+y=3.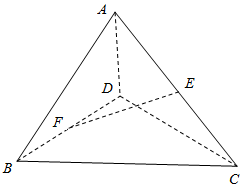 空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.
空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.