题目内容
7.已知一曲线C是与两个定点O(0,0),A(3,0)的距离比为$\frac{1}{2}$的点的轨迹.(1)求曲线C的方程,并指出曲线类型;
(2)过(-2,2)的直线l与曲线C相交于M,N,且|MN|=2$\sqrt{3}$,求直线l的方程.
分析 (1)设M(x,y)是曲线上任意的一点,点M在曲线上的条件是$\frac{{|{MO}|}}{{|{MA}|}}=\frac{1}{2}$,由两点间距离公式,转化求解轨迹方程即可.
(2)当直线l斜率不存在时,$|{MN}|=2\sqrt{3}$,求出x.当直线l斜率存在时,设直线l的方程为y-2=k(x+2),即kx-y+2k+2=0,求出圆心到此直线的距离为$d,d=\sqrt{{2^2}-3}=1$,求出k,即可得到所求的直线l的方程.
解答 解:(1)设M(x,y)是曲线上任意的一点,点M在曲线上的条件是$\frac{{|{MO}|}}{{|{MA}|}}=\frac{1}{2}$.-------(2分)
由两点间距离公式,上式用坐标表示为$\sqrt{{x^2}+{y^2}}=\frac{1}{2}\sqrt{{{(x-3)}^2}+{y^2}}$,
整理得:x2+y2+2x-3=0,(x+1)2+y2=4--------(5分)
曲线C是以(-1,0)为圆心,以2为半径的圆.------(6分)
(2)当直线l斜率不存在时,$|{MN}|=2\sqrt{3}$,∴x=-2-----(8分)
当直线l斜率存在时,设直线l的方程为y-2=k(x+2),即kx-y+2k+2=0,
设圆心到此直线的距离为$d,d=\sqrt{{2^2}-3}=1$,∴$1=\frac{{|{-k+2k+2}|}}{{\sqrt{{k^2}+1}}},k=-\frac{3}{4}$,
所以直线l的方程:$y-2=-\frac{3}{4}(x+2),即3x+4y-2=0$,
直线l的方程:∴x=-2或3x+4y-2=0.-------(12分)
点评 本题考查轨迹方程的求法,直线与圆的位置关系的综合应用,考查转化思想以及计算能力.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | 2 | D. | $\sqrt{2}-1$ |
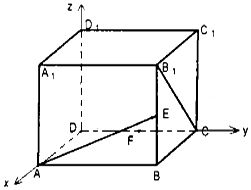 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,