题目内容
设关于正整数n的函数f(n)=1•22+2•32+…n(n+1)2
(1)求f(1),f(2),f(3);
(2)是否存在常数a,b,c使得f(n)=
(an2+bn+c)对一切自然数n都成立?并证明你的结论.
(1)求f(1),f(2),f(3);
(2)是否存在常数a,b,c使得f(n)=
| n(n+1) |
| 12 |
(1)∵f(n)=1•22+2•32+…n(n+1)2,
∴f(1)=1•22=4,
f(2)=1•22+2•32=22,
f(3)1•22+2•32+3•42=70;
(2)假设存在常数a,b,c使得f(n)=
(an2+bn+c)对一切自然数n都成立,
则f(1)=
(a+b+c)=4,
∴a+b+c=24①,
同理,由f(2)=22得4a+2b+c=44②,
由f(3)=70得9a+3b+c=70③
联立①②③,解得a=3,b=11,c=10.
∴f(n)=
(3n2+11n+10).
证明:1°当n=1时,显然成立;
2°假设n=k时,f(k)=
(3k2+11k+10)=
,
则n=k+1时,f(k+1)=f(k)+(k+1)[(k+1)+1]2
=
+(k+1)[(k+1)+1]2
=
(3k2+17k+24)
=
=
,
即n=k+1时,结论也成立.
综合1°,2°知,存在常数a=3,b=11,c=10使得f(n)=
(3n2+11n+10)对一切自然数n都成立.
∴f(1)=1•22=4,
f(2)=1•22+2•32=22,
f(3)1•22+2•32+3•42=70;
(2)假设存在常数a,b,c使得f(n)=
| n(n+1) |
| 12 |
则f(1)=
| 1×2 |
| 12 |
∴a+b+c=24①,
同理,由f(2)=22得4a+2b+c=44②,
由f(3)=70得9a+3b+c=70③
联立①②③,解得a=3,b=11,c=10.
∴f(n)=
| n(n+1) |
| 12 |
证明:1°当n=1时,显然成立;
2°假设n=k时,f(k)=
| k(k+1) |
| 12 |
| k(k+1)(k+2)(3k+5) |
| 12 |
则n=k+1时,f(k+1)=f(k)+(k+1)[(k+1)+1]2
=
| k(k+1)(k+2)(3k+5) |
| 12 |
=
| (k+1)(k+2) |
| 12 |
=
| (k+1)(k+2)(k+3)(3k+8) |
| 12 |
=
| (k+1)[(k+1)+1][(k+2)+1][3(k+1)+5] |
| 12 |
即n=k+1时,结论也成立.
综合1°,2°知,存在常数a=3,b=11,c=10使得f(n)=
| n(n+1) |
| 12 |

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
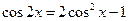 (
(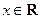 )的两边求导,得:
)的两边求导,得: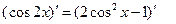 ,
,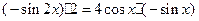 ,化简得等式:
,化简得等式: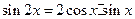 。
。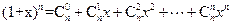 (
(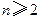 ),证明:
),证明: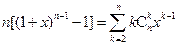 。
。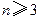 ,求证:
,求证: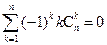 ; (ii)
; (ii)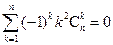 ; (iii)
; (iii)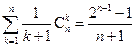 。
。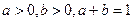 求证:
求证: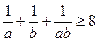 (用两种方法证明).
(用两种方法证明). 、
、 ,定义
,定义 ,其中
,其中 是
是 、
、 、
、 ,有如下四个命题:
,有如下四个命题: ;
; ;
; ;
; .
.



 是虚数单位,
是虚数单位, ,若复数
,若复数 的实部是
的实部是 ,则
,则 .
.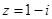 (
(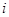 为虚数单位),则复数
为虚数单位),则复数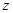 的模
的模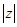 = .
= . 的共轭复数
的共轭复数 等于( )
等于( )


