题目内容
将4个新转入的学生分到高二的4个指定的班,每班分入的人数不限
(1)求这4个班各分到1个新生的概率
(2)求至少有1个班未分到新生的概率
(3)求其中恰有1个班未分到新生的概率.
(1)求这4个班各分到1个新生的概率
(2)求至少有1个班未分到新生的概率
(3)求其中恰有1个班未分到新生的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:先求出4个新转入的学生分到高二的4个指定的班的总数为44=256种,再分别求出满足条件的基本事件,根据概率公式计算即可
解答:
解:4个新转入的学生分到高二的4个指定的班的总数为44=256种,
(1)这4个班各分到1个新生,有
=24种,故这4个班各分到1个新生的概率P=
=
(2)至少有1个班未分到新生,它的对立事件为每个班都分到学生,根据互斥事件的概率公式,得到至少有1个班未分到新生的概率1-
=
;
(3)其中恰有1个班未分到新生,从四个班级先选一个班级,再把4名学生分到3个班级中,共有
•
•
=144种,
故其中恰有1个班未分到新生的概率P=
=
(1)这4个班各分到1个新生,有
| A | 4 4 |
| 24 |
| 256 |
| 3 |
| 32 |
(2)至少有1个班未分到新生,它的对立事件为每个班都分到学生,根据互斥事件的概率公式,得到至少有1个班未分到新生的概率1-
| 3 |
| 32 |
| 29 |
| 32 |
(3)其中恰有1个班未分到新生,从四个班级先选一个班级,再把4名学生分到3个班级中,共有
| C | 1 4 |
| C | 2 4 |
| A | 3 3 |
故其中恰有1个班未分到新生的概率P=
| 144 |
| 245 |
| 9 |
| 16 |
点评:本题考查了古典概型概率问题,关键是求出满足条件的基本事件,属于中档题

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、?α、β∈R,使sin(α+β)=sinα+sinβ |
| B、?a>0,函数f(x)=ln2x+lnx-a有零点 |
| C、?ϕ∈R,函数f(x)=sin(2x+ϕ)都不是偶函数 |
| D、?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上单调递减 |
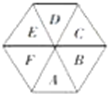 在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.
在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.(1)现有2种不同的植物可供选择,则有种栽
(2)现有4种不同的植物可供选择,则有
下列命题中的假命题是( )
| A、?x∈R,lnx=0 | ||
B、?x∈R,tanx=
| ||
| C、?x∈R,x2>0 | ||
| D、?x∈R,3x>0 |
为了解2000名学生对学校食堂的意见,准备从中抽取一个样本容量为50的样本.若采用系统抽样,则分段间隔k为( )
| A、20 | B、30 | C、40 | D、50 |