题目内容
13. 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其中O为坐标原点.
(1)求椭圆的标准方程;
(2)证明:△OAB的面积是一个常数.
分析 (1)运用椭圆的离心率公式和点满足椭圆方程,解得a=2,b=1,可得椭圆方程;
(2)设A(x1,y1),B(x2,y2),M(m,n),可得x12+4y12=4,x22+4y22=4,m2+4n2=4,由向量的坐标表示,求得m,n,再平方相加,可得x1x2+4y1y2=0,再由椭圆的参数方程,结合两角差的正弦和余弦公式,化简整理,即可得到常数1.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
将点 $(\frac{6}{5},\frac{4}{5})$代入椭圆方程,可得$\frac{36}{25{a}^{2}}$+$\frac{16}{25{b}^{2}}$=1,
又a2-b2=c2,
解得a=2,b=1,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)证明:设A(x1,y1),B(x2,y2),M(m,n),
可得x12+4y12=4,x22+4y22=4,m2+4n2=4,
由$\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,
可得(m,n)=cosα•(x1,y1)+sinα•(x2,y2),
即有m=cosα•x1+sinα•x2,
n=cosα•y1+sinα•y2,
可得m2+4n2=cos2α(x12+4y12)+sin2α(x22+4y22)+2cosαsinα(x1x2+4y1y2)
=4cos2α+4sin2α+sin2α(x1x2+4y1y2),
即有sin2α(x1x2+4y1y2)=0,由α∈(0,$\frac{π}{2}$),可得
x1x2+4y1y2=0,
又S△ABO=$\frac{1}{2}$|OA|•|OB|sin∠AOB=$\frac{1}{2}$$\sqrt{|OA{|}^{2}•|OB{|}^{2}-(|OA|•|OB|cos∠AOB)^{2}}$
=$\frac{1}{2}$$\sqrt{({{x}_{1}}^{2}+{{y}_{1}}^{2})({{x}_{2}}^{2}+{{y}_{2}}^{2})-({x}_{1}{x}_{2}+{y}_{1}{y}_{2})^{2}}$=$\frac{1}{2}$|x1y2-x2y1|,
由x1=2cosβ,y1=sinβ,x2=2cosγ,y2=sinγ,
x1x2+4y1y2=0,即为4(cosβcosγ+sinβsinγ)=0,
即cos(β-γ)=0,
又S△ABO=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$|2cosβsinγ-2cosγsinβ|=|sin(β-γ)|=1.
则△OAB的面积是一个常数1.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查三角形的面积为常数,注意点在椭圆上满足椭圆方程,以及平方相加,同时结合椭圆的参数方程和三角形的面积公式,考查运算能力,属于中档题.

| A. | f(1)<f(-1)<f(0) | B. | f(0)<f(1)<f(-1) | C. | f(-1)<f(0)<f(1) | D. | f(1)<f(0)<f(-1) |
| A. | 14 | B. | 25 | C. | 35 | D. | 40 |

| A. | 10 | B. | 13 | C. | -10 | D. | -13 |
 如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).
如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).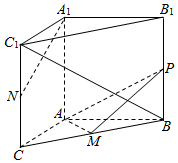 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.