题目内容
8. 如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).
如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).
分析 在△ABD中使用正弦定理求出AD,在△ACD中利用正切函数的定义解出CD.
解答 解:在△ABD中,∠ADB=180°-110°-40°=30°,
由正弦定理得$\frac{AB}{sin∠ADB}=\frac{AD}{sinB}$,即$\frac{800}{\frac{1}{2}}=\frac{AD}{sin40°}$,解得AD=1028.46m.
在Rt△ACD中,∵tan∠CAD=$\frac{CD}{AD}$,∴CD=AD•tan∠CAD=1028.46×tan25°≈480m.
∴山高CD约为480m.
点评 本题考查了解三角形的实际应用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
19.i是虚数单位,复数$\frac{2i}{1+i}$的虚部为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
16.已知x,y满足$\left\{\begin{array}{l}x≥1\\ x+y≤4\\ x-2y-1≤0\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
3.运行如图所示的程序框图后,输出的m值是( )
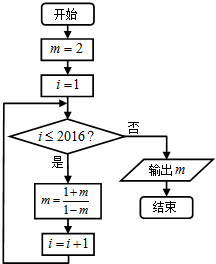

| A. | -3 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
17.一个三位自然数$\overline{abc}$的百位,十位,个位上的数字依次为a,b,c,当且仅当a>b且c>b时称为“凹数”.若a,b,c∈{4,5,6,7,8},且a,b,c互不相同,任取一个三位数$\overline{abc}$,则它为“凹数”的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
18.已知向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(3,x)$,$\overrightarrow c=(x,4)$,若$(\overrightarrow a-\overrightarrow b)∥\overrightarrow c$,则x=( )
| A. | 2或-4 | B. | -2或4 | C. | $\frac{2}{3}$ | D. | $-\frac{2}{3}$ |
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其